Question

Explain the analytical method for vector addition to find the resultant vector.

Answer 1

Hint: Analytical methods of vector addition and subtraction use geometry and basic trigonometry. Part of the graphical approach is preserved, because for simple visualization, vectors are still represented by arrows.

Complete answer:

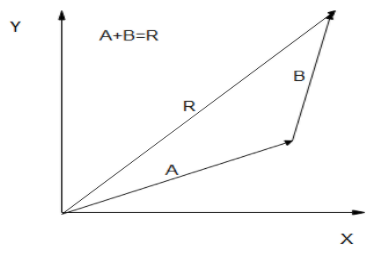
If $A$ and $B$ represent two legs of a walk (two displacements), then $R$ is the total displacement. The person taking the walk ends up at the tip of $\mathrm{R}$. There are many ways to arrive at the same point. In particular, the person could have walked first in the x-direction and then in the $y$ -direction. Those paths are the $x$ - and $y$ components of the resultant, $R_{x}$ and $R_{y} .$ If we know $R_{x}$ and $R_{y},$ we can find $R$ and $\theta$ using the equations $A=\sqrt{A_{x}^{2}+A_{y}^{2}}$ and $\theta ={{\tan }^{-1}}\left( \dfrac{{{A}_{Y}}}{{{A}_{x}}} \right).$ When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.
Steps To be Followed:
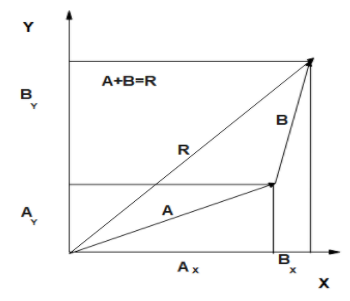
1.Identify the $x$ - and $y$ -axes that will be used in the problem. Then, find the components of each vector to be added along the chosen perpendicular axes. Use the equations $A_{x}=A \cos \theta$ and $A_{y}=A \sin \theta$ to find the components. In Figure, these components are $A_{x}, A_{y}, B_{x},$ and $B_{y} .$ The angles that vectors $A$ and $B$ make with the $x$ -axis are $\theta_{A}$ and $\theta_{B},$ respectively.

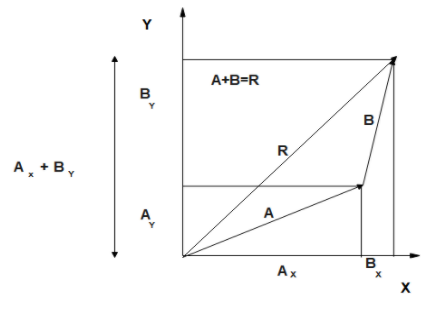
2.Find the resulting components along each axis by adding the individual vector components along that axis.
$R_{x}=A_{x}+B_{x}$
$R_{y}=A_{y}+B_{y}$

3.To get the magnitude $R$ of the resultant, use the Pythagorean theorem:
$R=\sqrt{R_{x}^{2}+R_{y}^{2}}$
4. To get the direction of the resultant:
$\theta ={{\tan }^{-1}}\left( \dfrac{{{R}_{Y}}}{{{R}_{X}}} \right)$
\[\therefore \] The resultant vector using the analytical method for vector addition is $R=\sqrt{R_{x}^{2}+R_{y}^{2}}$

Note:
Analytical methods, however, are more succinct, descriptive, and reliable than graphical methods, which are constrained by the precision with which a drawing can be produced. Only the precision and accuracy with which physical quantities are understood is constrained by analytical methods.