Question

Explain simple microscope on the basis of the following points:
(a) Ray diagram for the formation of image;
(b) Expression for magnifying power when the final image is formed: (i) At the least distance of distinct vision; (ii) At infinity.

Answer 1

Hint: Lens used in a simple microscope is a convex lens, it forms a virtual, erect and magnified image at distance of distinct vision. In this way you can imagine a diagram by knowing the idea of a convex lens. Magnifying power is defined as ratio of angle subtended at eye by the image and angle subtended at unaided eye by the object at distance of distinct vision. Put the values in magnifying power formula and get magnifying power formula for image at DDV and image at infinity.

Complete step by step answer:

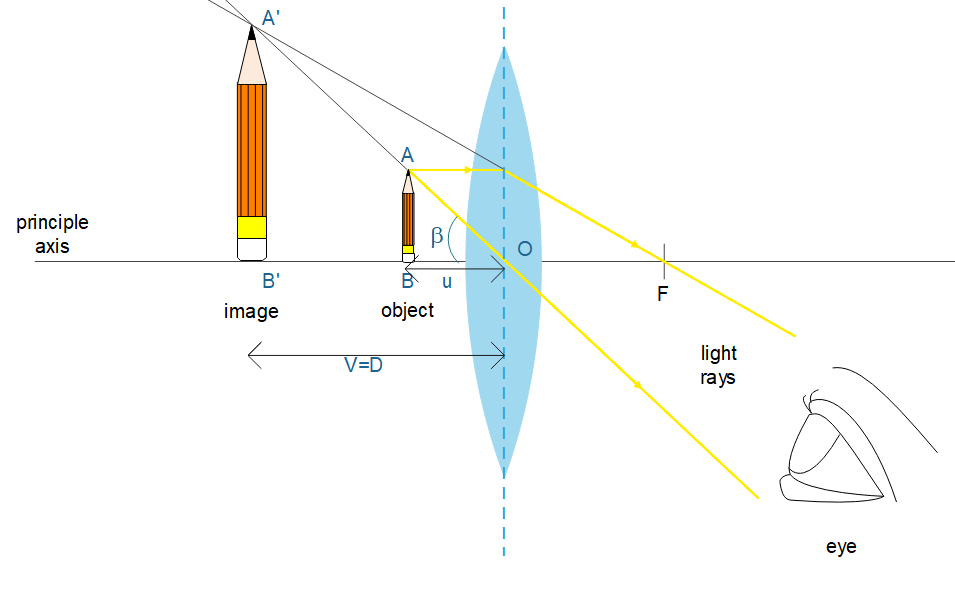
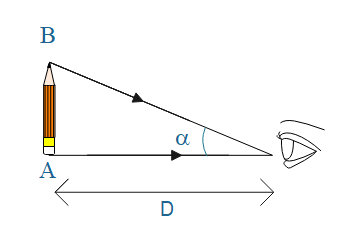
The magnifying power of a simple microscope is defined as the ratio of the angle subtended at eye by the image to the angle subtended at unaided eye by the object kept at distance of distinct image (DDV).
$\begin{align}
  & \text{M}\text{.P}\text{. =}\dfrac{\text{angle subtended at eye by the image}}{\text{Angle subtended at unaided eye by the object at DDV}} \\
 & \text{M}\text{.P}\text{. =}\dfrac{\beta }{\alpha }----(1) \\
\end{align}$
Where $\beta $ is the angle subtended at the eye by the image\[A'B'\]and$\alpha $is the angle subtended at the eye by the object kept at DDV.
\[\begin{align}
  & \text{Consider }\vartriangle \text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ O,} \\
 & \text{tan}\beta \text{=}\dfrac{A'B'}{OB'}=\dfrac{AB}{u} \\
 & \text{since}\beta \text{ is very small-tan}\beta \approx \text{ }\beta \text{=}\dfrac{AB}{u} \\
\end{align}\]
\[\begin{align}
  & \text{tan}\alpha \text{=}\dfrac{AB}{D} \\
 & \text{since}\alpha \text{ is very small-tan}\alpha \approx \alpha \text{=}\dfrac{AB}{D} \\
\end{align}\]
Put value in equation (1), we get
$M.P.=\dfrac{\dfrac{AB}{u}}{\dfrac{AB}{D}}=\dfrac{D}{u}$
From lens formula we have: $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
According to sign convention. Here $u\text{ and }v$ are negative and $f$is positive,
Therefore we get-
$\begin{align}
  & \dfrac{1}{u}=\dfrac{1}{v}+\dfrac{1}{f} \\
 & \dfrac{D}{u}=\dfrac{D}{v}+\dfrac{D}{f} \\
 & M.P.=\dfrac{D}{v}+\dfrac{D}{f} \\
\end{align}$
This equation gives the magnifying power of a simple microscope.
Case (i): If the image is formed at distance of distinct vision i.e. DDV i.e\[v=D\], then
$M.P.=\dfrac{D}{D}+\dfrac{D}{f}=\left( 1+\dfrac{D}{f} \right)$
Hence magnifying power is $\left( 1+\dfrac{D}{f} \right)$, if the image formed at distance of distinct vision.
Case (ii): If the image is formed at infinity i.e. $v=\infty ;$then
$M.P.=\dfrac{D}{\infty }+\dfrac{D}{f}=\left( \dfrac{D}{f} \right)$
Hence magnifying power is $\dfrac{D}{f}$, if the image formed at infinity.

Note:
From above two cases, we can say that magnifying power of simple microscope can be anything from$\left( \dfrac{D}{f} \right)to\left( 1+\dfrac{D}{f} \right)$.
Thus the magnifying power of a simple microscope is inversely proportional to focal length and it is maximum when the image is at a distance of distinct vision.