Question

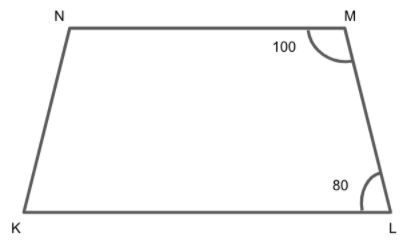
Explain how this figure is a trapezium. Which of its two sides is parallel?

Answer 1

Hint:
First, we will extend the line segment LM to O. We know that for line segments NM and KL, the sum of interior angles on the same side of transversal is 180 degrees, which is only possible if the lines are parallel lines.

Complete step by step solution:
We are given that a quadrilateral KLMN have \[\angle {\text{NML = 100}}^\circ \] and \[\angle {\text{MLK = 80}}^\circ \].

Extend the line segment LM to O.

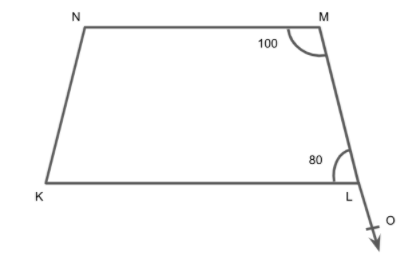
We know that for line segments NM and KL, a transversal line MO is intersecting two given lines such that their sum is 180 degrees.

Finding the sum of angles \[\angle {\text{NML}}\] and \[\angle {\text{MLK}}\], we get

\[ \Rightarrow 100^\circ + 80^\circ {\text{ = 180}}^\circ \]

Thus, the sum of interior angles on the same side of transversal is 180 degrees, which is only possible if NM and KL are parallel lines.

Therefore, we have that \[{\text{NM}}||{\text{KL}}\].

Since KLMN is a quadrilateral with a pair of parallel lines, that is, \[{\text{NM}}||{\text{KL}}\].

Hence, \[{\text{KLMN}}\] is a trapezium.

Note:
In solving these types of questions, you should know that a trapezium is a type of quadrilateral, which has only two parallel sides and the other two sides are non-parallel. The possibility of error in this question can be that you assume the sum is equal to 90 degrees, which is wrong. If the non-parallel sides of a trapezium are equal then it is called an isosceles trapezium. We will draw the diagram for better understanding of this problem. We have to prove it to be a trapezium so before that, we will only call it a quadrilateral with four sides.