Question

Explain how a square is:
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle

Answer 1

Hint: As we know that, in square all sides are equal in length and each angle is equal to. The diagonals are equal and bisect each other.

Complete step-by-step solution:
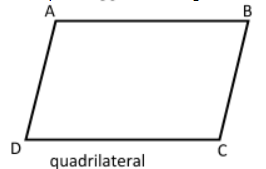
(i) Properties of quadrilateral:
(a) A quadrilateral should be closed shaped with $4$sides.
(b) The sum of angle is${360^o}$.
Properties of square:
(a) square has also $4$sides.
(b) Each angle is ${90^o}$ i.e. sum of the angle is${360^o}$.
$\therefore $Square is a quadrilateral.

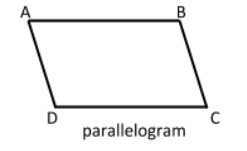
(ii) Properties of parallelogram:
(a) A parallelogram has both pairs of opposite sides are equal in length and parallel.
(b) Diagonal bisect each other.
Properties of square:
(a) A square with both pairs of opposite sides are equal in length and parallel.
(b) Diagonal bisect each other at${90^o}$.
$\therefore $Square is also a parallelogram.

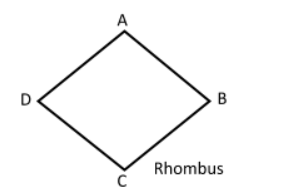
(iii) Properties of rhombus:
(a) A rhombus is a parallelogram.
(b) All sides are equal.
(c) Diagonals bisect each other at ${90^o}$.
Properties of square:
(a) A square is a parallelogram.
(b) All sides are equal.
(c) Diagonal bisect each other at ${90^o}$.
$\therefore $ A square is a rhombus.

(iv) Properties of rectangle:
(a) All angles are equal i.e. ${90^o}$.
(b) Diagonals bisect each other.
(c) It is a parallelogram.
Properties of square:
(a) All angles are equal i.e.${90^o}$.
(b) Diagonals bisect each other at${90^o}$.
(c) It is also a parallelogram.
$\therefore $A square is a rectangle.

Note:As we know that a quadrilateral is a $4$sided \[2 - \]dimensional figure whose sum of internal angles is ${360^o}$.