Question

Explain how a square is a,
( a ) quadrilateral
( b ) parallelogram
( c ) rhombus
( d ) rectangle

Answer 1

Hint: One object is the same as another object if they both possess the same properties. What we will do is discuss properties of parallelogram, quadrilateral, rhombus and rectangle and check whether squares satisfy all these properties or not.

Complete step-by-step answer:

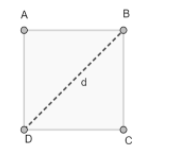
A square is a four sided polygon whose all four sides are the same and all four angles made by adjacent sides are equal to ${{90}^{{}^\circ }}$ .
Now from the diagram, let there be a square ABCD with four sides namely AB, BC, CD and DA with diagonal d and angles $\angle ABC,\angle BCD,\angle CDA,\angle DAC$ .
Now, we have to prove that the square is quadrilateral, parallelogram, rhombus and rectangle.
What we will do is we will check whether the square satisfies all minimum required properties to be , parallelogram, rhombus and rectangle.
Now, what quadrilateral is, it is a polygon with four sides and four vertices. Quadrilaterals can take any shape but the only condition is that the polygon must have four sides and four vertices.
Now, from the figure we can see that square ABCD has four sides namely AB, BC, CD and DA and four vertices namely A, B, C and D. Hence, the square is quadrilateral.
Now, parallelogram is a quadrilateral with two pairs of parallel sides, the opposite facing sides are equal and the opposite angles of a parallelogram are of equal measure. Now, in square all four sides are the same hence all opposite sides are equal and all sides are of angle ${{90}^{{}^\circ }}$ so opposite angles are also equal. Hence, the square is a parallelogram.
Now, rhombus is quadrilateral whose all four sides are equal and opposite angles are equal. In square, all four sides are equal and opposite sides are also equal whose measure is ${{90}^{{}^\circ }}$. Hence, the square is rhombus.
Now, the rectangle is a quadrilateral whose opposite sides are equal and all four angles are of ${{90}^{{}^\circ }}$ in measure. Since, all sides of the square are equal so opposite sides are equal and the measure of all four angles are equal to ${{90}^{{}^\circ }}$. Hence, the square is a rectangle.

Note: Properties of square, parallelogram, quadrilateral, rhombus and rectangle must be kept in mind. We need to satisfy only those conditions of parallelogram, quadrilateral, rhombus and rectangle for squares which are minimum required.