Question

Every rational number is an integer.
a) True
b) False

Answer 1

Hint: Think of the basic definition of integers and rational numbers and try to figure out the relation. Use the Venn diagram to represent the sets of rational numbers and integers to get a better visualization of the relation between them.

Complete step-by-step answer:

First, let us try to recall the definition of integer.

So, the basic definition of integer is “all the rational numbers which can be written without the use of any fractional component no matter whether it’s positive or negative is termed as integers.”

Now, moving on to rational numbers, rational numbers are defined as a set of numbers, which can be expressed in the form $\dfrac{p}{q}$ , where both p and q are integers and q is not equal to 0.

So, from the above definitions, we can say:

“All integers numbers are rational numbers, but all rational numbers are not integers.”

If we think in terms of sets, then rational numbers can be denoted by R and is given by:

$R=\left\{ -\infty ,......\dfrac{-2}{3},\dfrac{-1}{7},0,1,2,\dfrac{14}{3}....\infty \right\}$

Also, we can denote the set of integers as Z and is given by:

Z = { $-\infty $ , ……….. -1, 0, 1, 2, 3, ……………………. $\infty $ }

This can be represented in the form of a Venn diagram as:

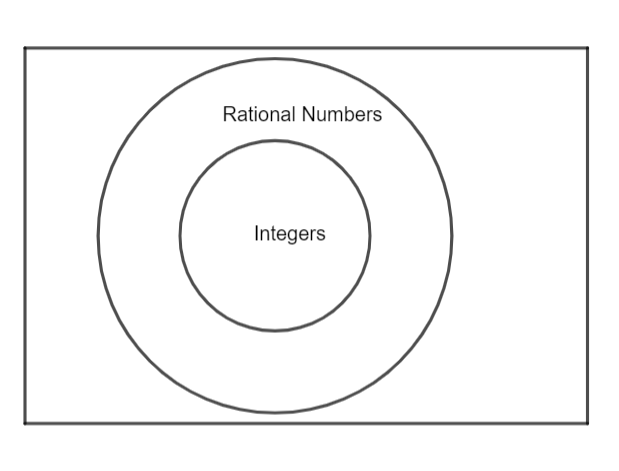
But the statement given in the question “Every rational number is an integer, “ which states the opposite of what we get from the definition. So, the statement is False.
So, the answer to the question is False.

Note: Always read the question twice as there is a high probability that the phrases used might give you a wrong idea at your 1st call, as in such statements, the change of single words may change your answer. For example: in this statement, if you replace “Every” by “Some” the answer is changed. Also, be very sharp with the definitions of the terms as they might be confusing.