
Evaluate using long division method: \[\sqrt {6241} \]
Answer
610.8k+ views
Hint: A square root of a number is a value that, when multiplied by itself, gives the number. Recall the method to find the square root by long division and find the value of the square root of 6241.
Complete step-by-step answer:
The square root of a number is another number that produces the first number when it is multiplied by itself. For example, the square root of 25 is 5 because 5 multiplied with 5 is 25.
Sometimes, it is obvious to find the square root of a number, usually a smaller number but other times, the number might be big or decimal and we need to use a method called long division to arrive at the answer.
In this problem, we need to find the square root of 6241.
As the first step in long division, we need to pair the digits from the right.
Hence, we pair 4 and 1 as 41, and we pair 6 with 2 to get 62.
\[62{\text{ }}41\]
Next, we need to find the largest integer such that its square is less than the first paired number.
We know that \[{7^2}\] is 49, which is the largest square number less than 62. Then, we have:
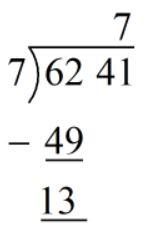
Now, we bring the next pair down and the number becomes 1341, we now need to find a digit x such that the three-digit number 14x when multiplied with x gives 1341.
We know that 149 multiplied with 9 gives 1341, then we have:

Hence, the square root of 6241 is 79.
Note: You can cross-check your answer by squaring the final answer to check if it results in 6241. You can use the trick that any number ending with 9 when multiplied with another number ending with 9, the units place is 1.
Complete step-by-step answer:
The square root of a number is another number that produces the first number when it is multiplied by itself. For example, the square root of 25 is 5 because 5 multiplied with 5 is 25.
Sometimes, it is obvious to find the square root of a number, usually a smaller number but other times, the number might be big or decimal and we need to use a method called long division to arrive at the answer.
In this problem, we need to find the square root of 6241.
As the first step in long division, we need to pair the digits from the right.
Hence, we pair 4 and 1 as 41, and we pair 6 with 2 to get 62.
\[62{\text{ }}41\]
Next, we need to find the largest integer such that its square is less than the first paired number.
We know that \[{7^2}\] is 49, which is the largest square number less than 62. Then, we have:
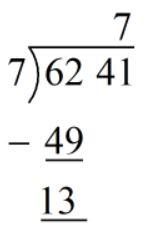
Now, we bring the next pair down and the number becomes 1341, we now need to find a digit x such that the three-digit number 14x when multiplied with x gives 1341.
We know that 149 multiplied with 9 gives 1341, then we have:

Hence, the square root of 6241 is 79.
Note: You can cross-check your answer by squaring the final answer to check if it results in 6241. You can use the trick that any number ending with 9 when multiplied with another number ending with 9, the units place is 1.
Recently Updated Pages
Which part of the earth is ahead in terms of time A class 6 social science CBSE

Which dynasty was ruling Magadha at the time of Alexander class 6 social science CBSE

The hymns in the Vedas have been referred to as which class 6 social science CBSE

Form the smallest 8digit number using the digits 5 class 6 maths CBSE

What is the full form of GMT A Greenwich Mean Time class 6 social science CBSE

Fill in the blanks with the most appropriate words class 6 english CBSE

Trending doubts
How many millions make a billion class 6 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Number of Prime between 1 to 100 is class 6 maths CBSE

The planet nearest to earth is A Mercury B Venus C class 6 social science CBSE

What is the shape of Earth A Circle B Square C Sphere class 6 social science CBSE

Why is the Earth called a unique planet class 6 social science CBSE





