Question

How do you evaluate the integral $\sin \left( {{x}^{2}}+{{y}^{2}} \right)dr$ where r is the region $9\le {{x}^{2}}+{{y}^{2}}\le 64$in the polar form?

Answer 1

Hint: In 2 dimensional we convert into polar coordinate as $\left( r,\theta \right)$ where r is the distance from origin to the point (x,y) ,$\theta $ is the angle between positive x axis and line joining origin and the point (x,y) . So the value of r is $\sqrt{{{x}^{2}}+{{y}^{2}}}$ . First we will convert the equation we have to integrate into polar form and then we can write $dxdy$ as $rdrd\theta $ and change the limits

Complete step by step answer:
We have to integrate $\sin \left( {{x}^{2}}+{{y}^{2}} \right)$ in the region $9\le {{x}^{2}}+{{y}^{2}}\le 64$
We can write $\int{\sin \left( {{x}^{2}}+{{y}^{2}} \right)}dxdy$ in the region $9\le {{x}^{2}}+{{y}^{2}}\le 64$
Drawing the region in graph

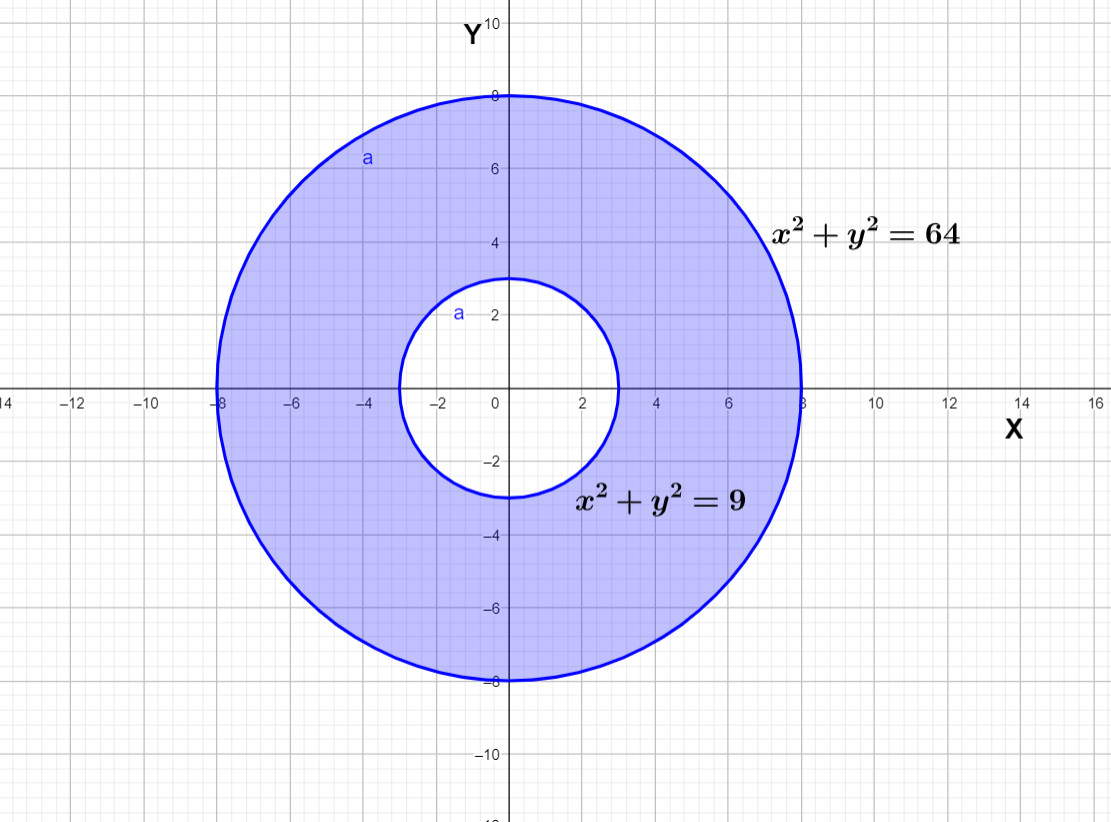
We can see that all quadrants have same area and all are symmetric so we can compute the integration for first quadrant and multiply it by 4
If we convert the region in parametric form then it would be $rdrd\theta $ where r is from 3 to 8 and $\theta $ is from 0 to $\dfrac{\pi }{2}$
We can write ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$
So $\int{\sin \left( {{x}^{2}}+{{y}^{2}} \right)}dxdy$ in the region $9\le {{x}^{2}}+{{y}^{2}}\le 64$ = $4\times \int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{\int\limits_{r=3}^{r=8}{\sin {{r}^{2}}rdrd\theta }}$
First we will integrate with respect to r and then with respect to $\theta $
We can integrate $\sin {{r}^{2}}rdr$ by taking ${{r}^{2}}$ as t so the value of $rdr$ will be equal to $\dfrac{dt}{2}$
So we can write $\int{\sin {{r}^{2}}rdr=\int{\dfrac{1}{2}\sin t}dt}$
The value of $\int{\dfrac{1}{2}\sin tdt}$ is equal to $-\dfrac{1}{2}\cos t$ , replacing t with ${{r}^{2}}$ we get $-\dfrac{1}{2}\cos {{r}^{2}}$
So the value of $\int\limits_{r=3}^{r=8}{\sin {{r}^{2}}rdr}$ is equal to $-\dfrac{1}{2}\left[ \cos \left( {{8}^{2}} \right)-\cos \left( {{3}^{2}} \right) \right]$ = $\dfrac{1}{2}\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]$
We can write $4\times \int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{\int\limits_{r=3}^{r=8}{\sin {{r}^{2}}drd\theta }}$ as $4\times \int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{\dfrac{1}{2}\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]d\theta }$
$\Rightarrow 4\times \int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{\dfrac{1}{2}\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]d\theta }=2\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]\int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{d\theta }$
$\Rightarrow 4\times \int\limits_{\theta =0}^{\theta =\dfrac{\pi }{2}}{\dfrac{1}{2}\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]d\theta }=2\times \dfrac{\pi }{2}\left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]=\pi \left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]$
 $\pi \left[ \cos \left( {{3}^{2}} \right)-\cos \left( {{8}^{2}} \right) \right]$=$\pi \left[ \cos \left( 9 \right)-\cos \left( 64 \right) \right]$
So the value of integral $\sin \left( {{x}^{2}}+{{y}^{2}} \right)dr$ where r is the region $9\le {{x}^{2}}+{{y}^{2}}\le 64$ is equal to $\pi \left[ \cos \left( 9 \right)-\cos \left( 64 \right) \right]$

Note:
In this type of problem we need set the limit of r and $\theta $ very carefully, it is given that $9\le {{x}^{2}}+{{y}^{2}}\le 64$ and ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ so $9\le {{r}^{2}}\le 64$ so the limit of r is from 3 to 8. The limit of $\theta $ is from $\dfrac{\pi }{2}$ as we integrate in the first quadrant. Converting into polar form is very important process write x as $r\sin \theta $ and y as $r\sin \theta $, and write the term ${{x}^{2}}+{{y}^{2}}$ as ${{r}^{2}}$ .