Question

Evaluate the following Trigonometric function:
$\dfrac{\sin 30{}^\circ -\sin 90{}^\circ +2\cos 0{}^\circ }{\tan 30{}^\circ \tan 60{}^\circ }$

Answer 1

Hint: All the angles used in the expression given in the question are standard angles so, we know the values of the trigonometric ratios given in the question; just use it and simplify to reach the answer.

Complete step by step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

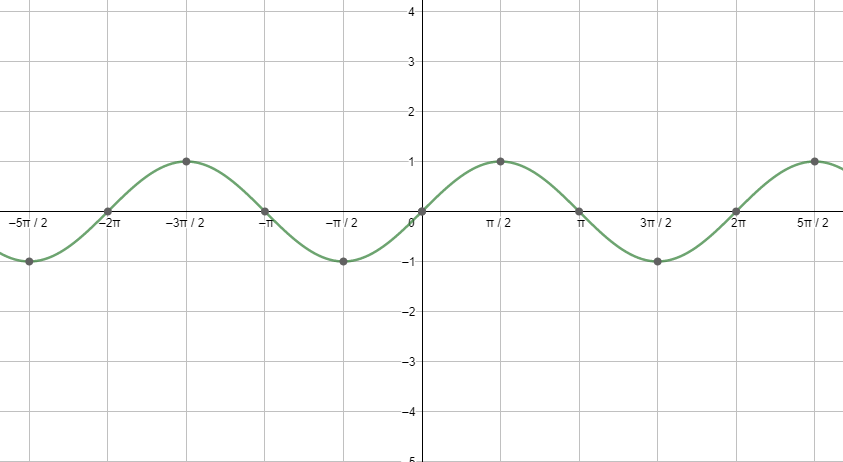
Next, let us see the graph of cosx.

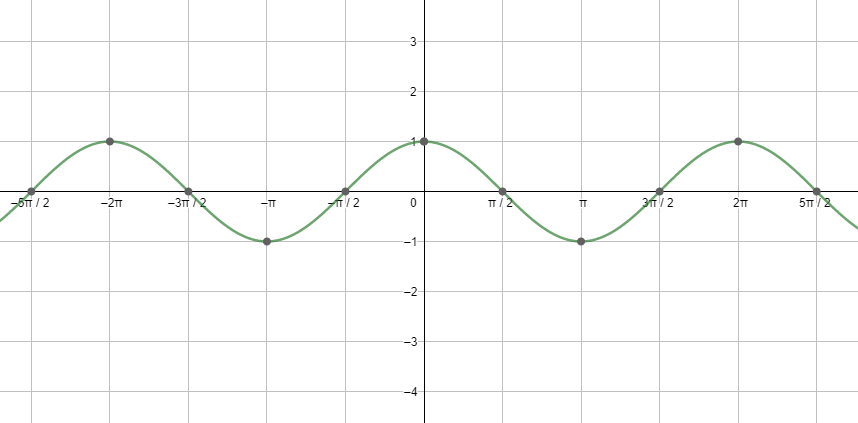
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ $
We will now solve the equation given in the question.
$\dfrac{\sin 30{}^\circ -\sin 90{}^\circ +2\cos 0{}^\circ }{\tan 30{}^\circ \tan 60{}^\circ }$
Now we know $\sin 30{}^\circ =\dfrac{1}{2},\text{ sin90}{}^\circ \text{=1, cos0}{}^\circ \text{=1, tan30}{}^\circ \text{=}\dfrac{1}{\sqrt{3}},\text{ tan60}{}^\circ \text{=}\sqrt{3}$ . On putting these values in our expression, we get
 $\dfrac{\dfrac{1}{2}-1+2}{\dfrac{1}{\sqrt{3}}\times \sqrt{3}}=\dfrac{1}{2}+1=\dfrac{3}{2}$
Therefore, the answer to the expression in the above question is $\dfrac{3}{2}$ .

Note: It is useful to remember the graph of the trigonometric ratios along with the signs of their values in different quadrants. For example: sine is always positive in the first and the second quadrant while negative in the other two. Also, remember the property of complementary angles of trigonometric ratios along with the values of trigonometric ratios of standard angles.