
Evaluate the following limit, $\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}$ .
Answer
529.8k+ views
Hint: First, we should take logarithms and simplify it into two decomposed limits. We may need to use the graph of $\ln x$. Then we should solve these two limits individually, and finally take exponential to get our final answer.
Complete step by step answer:
Let us assume a variable L such that,
$L=\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}$
Let us now take logarithms on both sides of this equation. Thus, we get
$\ln L=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$
We know that for $x>0$, the function $\ln x$ is continuous, as obvious in the figure below,
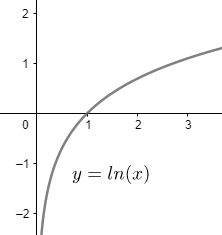
So, by the property of logarithms, we can easily write,
$\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$
Using this property, we can now write,
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)...\left( i \right)$
We know the property of logarithms that says,
$\log {{x}^{m}}=m\log x$
So, by using this property into equation (i), we can now say that
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \dfrac{1}{x}\ln x \right)...\left( ii \right)$
We know very well that limit is always distributive. So, we know that $\displaystyle \lim_{x \to a}\left( ab \right)=\displaystyle \lim_{x \to a}a\cdot \displaystyle \lim_{x \to a}b$
Hence, using this property of limits, we can write equation (ii) as,
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}\cdot \displaystyle \lim_{x \to {{0}^{+}}}\ln x...\left( iii \right)$
Now, let us assume 2 variables such that, $A=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}$ and $B=\displaystyle \lim_{x \to {{0}^{+}}}\ln x$. So, now we can write equation (iii) as
$\ln L=A\cdot B...\left( iv \right)$
Let us solve for A and B separately.
We have $A=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}$.
We know that when $x$ comes closer and closer to 0 from the right side, the value of A becomes larger and larger up to infinity.
Thus as $x$ tends to 0 or a very small positive number, the value of A tends to positive infinity.
Thus, we have $A=+\infty $.
We also have $B=\displaystyle \lim_{x \to {{0}^{+}}}\ln x$.
From the graph of $\ln x$ , we can see that as the value of $x$ comes closer and closer to 0 from the right side, the value of $\ln x$ becomes larger and larger but on the negative side.
Thus, we can say that as $x$ tends to 0 or very small positive numbers, the value of B tends to negative infinity.
Thus, we have $B=-\infty $.
Putting the values of A and B into equation (iv), we get
$\ln L=\left( \infty \right)\cdot \left( -\infty \right)$
$\Rightarrow \ln L=-\infty $
Now, taking exponentials on both sides of the equation, we get
${{e}^{\ln L}}={{e}^{-\infty }}$
$\Rightarrow L=0$
Thus, the value of $\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}$ is 0.
Note: We must always verify whether the function is continuous or not before applying $\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$. We must remember that any number raised to negative infinity is 0. And so, the term ${{e}^{-\infty }}$ is equal to 0.
Complete step by step answer:
Let us assume a variable L such that,
$L=\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}$
Let us now take logarithms on both sides of this equation. Thus, we get
$\ln L=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$
We know that for $x>0$, the function $\ln x$ is continuous, as obvious in the figure below,
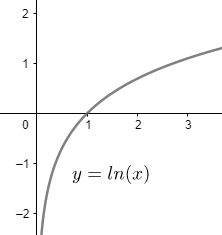
So, by the property of logarithms, we can easily write,
$\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$
Using this property, we can now write,
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)...\left( i \right)$
We know the property of logarithms that says,
$\log {{x}^{m}}=m\log x$
So, by using this property into equation (i), we can now say that
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \dfrac{1}{x}\ln x \right)...\left( ii \right)$
We know very well that limit is always distributive. So, we know that $\displaystyle \lim_{x \to a}\left( ab \right)=\displaystyle \lim_{x \to a}a\cdot \displaystyle \lim_{x \to a}b$
Hence, using this property of limits, we can write equation (ii) as,
$\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}\cdot \displaystyle \lim_{x \to {{0}^{+}}}\ln x...\left( iii \right)$
Now, let us assume 2 variables such that, $A=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}$ and $B=\displaystyle \lim_{x \to {{0}^{+}}}\ln x$. So, now we can write equation (iii) as
$\ln L=A\cdot B...\left( iv \right)$
Let us solve for A and B separately.
We have $A=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}$.
We know that when $x$ comes closer and closer to 0 from the right side, the value of A becomes larger and larger up to infinity.
Thus as $x$ tends to 0 or a very small positive number, the value of A tends to positive infinity.
Thus, we have $A=+\infty $.
We also have $B=\displaystyle \lim_{x \to {{0}^{+}}}\ln x$.
From the graph of $\ln x$ , we can see that as the value of $x$ comes closer and closer to 0 from the right side, the value of $\ln x$ becomes larger and larger but on the negative side.
Thus, we can say that as $x$ tends to 0 or very small positive numbers, the value of B tends to negative infinity.
Thus, we have $B=-\infty $.
Putting the values of A and B into equation (iv), we get
$\ln L=\left( \infty \right)\cdot \left( -\infty \right)$
$\Rightarrow \ln L=-\infty $
Now, taking exponentials on both sides of the equation, we get
${{e}^{\ln L}}={{e}^{-\infty }}$
$\Rightarrow L=0$
Thus, the value of $\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}$ is 0.
Note: We must always verify whether the function is continuous or not before applying $\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)$. We must remember that any number raised to negative infinity is 0. And so, the term ${{e}^{-\infty }}$ is equal to 0.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




