Question

Evaluate the following
\[4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\]

Answer 1

Hint:First of all, consider the expression given in the question. Now make the table for trigonometric ratios of general angles. Now, from that find the values of \[\sin {{60}^{o}},\cos {{30}^{o}},\tan {{60}^{o}},\tan {{45}^{o}}\] and \[\cos {{45}^{o}}\] and substitute these in the given expression to get the required answer.

Complete step-by-step answer:
In this question, we have to find the value of the expression
\[4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\]
Let us consider the expression given in the question.
\[E=4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}....\left( i \right)\]
Now, we have to find the values of \[\sin {{60}^{o}},\cos {{30}^{o}},\tan {{60}^{o}},\tan {{45}^{o}}\] and \[\cos {{45}^{o}}\].
Let us make the table for trigonometric ratios of general angles like \[{{0}^{o}},{{30}^{o}},{{45}^{o}},{{60}^{o}},{{90}^{o}}\] and find the required values.

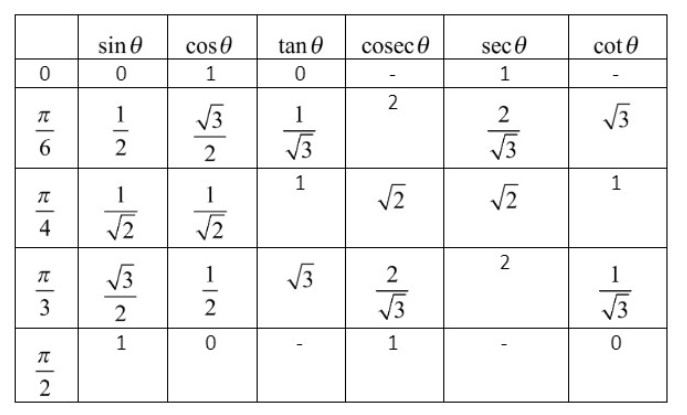
From the above table, we get, \[\sin {{60}^{o}}=\dfrac{\sqrt{3}}{2}\]. By substituting this in equation (i), we get,
\[E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\]
Also from the above table, we get \[\cos {{30}^{o}}=\dfrac{\sqrt{3}}{2}\]. By substituting this in the above equation, we get, \[E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\]
From the table, we also get, \[\tan {{60}^{o}}=\sqrt{3}\]. By substituting this in the above equation, we get,
\[E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\]
From the table, we also get, \[\tan {{45}^{o}}=1\]. By substituting this in the above equation, we get,
\[E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}} \right)+5{{\cos }^{2}}{{45}^{o}}\]
From the table, we also get, \[\cos {{45}^{o}}=\dfrac{1}{\sqrt{2}}\]. By substituting this in the above equation, we get,
\[E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}} \right)+5{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}\]
By simplifying the above equation, we get,
\[E=4\left( \dfrac{9}{16}+\dfrac{9}{16} \right)-3\left( 3-1 \right)+5\left( \dfrac{1}{2} \right)\]
\[E=4\left( \dfrac{18}{16} \right)-3\left( 2 \right)+\dfrac{5}{2}\]
\[E=\dfrac{18}{4}-6+\dfrac{5}{2}\]
\[E=\dfrac{9}{2}+\dfrac{5}{2}-6\]
\[E=\dfrac{14}{2}-6\]
\[E=7-6\]
\[E=1\]
Hence, we get the value of the expression \[4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}\] as 1.

Note: In these types of questions, students just need to remember the values of \[\sin \theta \] and \[\cos \theta \] at various angles like \[{{0}^{o}},{{30}^{o}},{{60}^{o}},{{45}^{o}},\] etc. and they can find \[\tan \theta \] by using \[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\]. Also, students must take care of substituting the corresponding angle. For example, if we have to find \[\tan {{60}^{o}}\], then we will use \[\sin {{60}^{o}}\] and \[\cos {{60}^{o}}\] while we have to find \[\tan {{45}^{o}}\], then we will use \[\sin {{45}^{o}}\] and \[\cos {{45}^{o}}\] and likewise. Also, it would also be better to memorize the trigonometric table.