
How do you evaluate the definite integral
Answer
499.8k+ views
Hint: Assume
Complete step-by-step solution:
Here, we have been provided with the integral
To solve this integral we need to remove the modulus sign from the given quadratic function. So, using the middle term split method we have,
Substituting
Representing these values on the number line along with the lower limit 0 and upper limit 4 of the given integral, we have,

Since, we have to find the integral from 0 to 4 so the values of x in the interval
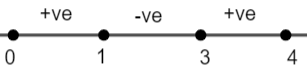
So, the given integral ‘I’ can be broken as: -
Substituting the values of limits and simplifying, we get,
Hence, the value of the integral is 4 square units.
Note: One may note that without removing the modulus sign we cannot find the integral value because we don’t know the sign of the function in certain intervals. Remember the basic approach that we have used to solve the question. The purpose of representing the values of x and the limits on the number line was to visualize the situation in a better way. Remember that the integration of a function denotes the area under the curve and the unit of area is square units, so it must be mentioned in the end.
Complete step-by-step solution:
Here, we have been provided with the integral
To solve this integral we need to remove the modulus sign from the given quadratic function. So, using the middle term split method we have,
Substituting
Representing these values on the number line along with the lower limit 0 and upper limit 4 of the given integral, we have,

Since, we have to find the integral from 0 to 4 so the values of x in the interval

So, the given integral ‘I’ can be broken as: -
Substituting the values of limits and simplifying, we get,
Hence, the value of the integral is 4 square units.
Note: One may note that without removing the modulus sign we cannot find the integral value because we don’t know the sign of the function in certain intervals. Remember the basic approach that we have used to solve the question. The purpose of representing the values of x and the limits on the number line was to visualize the situation in a better way. Remember that the integration of a function denotes the area under the curve and the unit of area is square units, so it must be mentioned in the end.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Hydrological cycle is controlled by A Grasslands B class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




