Question

How do you evaluate \[\tan \left( {\arcsin \left( {\dfrac{{12}}{3}} \right)} \right)\]?

Answer 1

Hint: We can solve this by taking \[\theta = \arcsin \left( {\dfrac{2}{3}} \right)\]. Here arcsine is inverse of sine. That is \[\arcsin = {\sin ^{ - 1}}\] and when we take sine on both sides, the inverse of the sine will get cancelled. We know the formula \[\operatorname{Sin} \theta = \dfrac{{{\text{Opposit side}}}}{{{\text{Hypoyenuse}}}}\] and \[\tan \theta = \dfrac{{{\text{Opposit side}}}}{{{\text{Adjacent side}}}}\]. Using some identity property we can also solve this.

Complete step-by-step answer:
Given, \[\tan \left( {\arcsin \left( {\dfrac{2}{3}} \right)} \right)\]
Let \[\theta = \arcsin \left( {\dfrac{2}{3}} \right)\].
Taking sine function on both sides we get,
\[ \Rightarrow \sin \theta = \dfrac{2}{3}\]
Using this we can find what is the value of tangent function. We can find this in two methods.
Let’s see the first method we know that \[\operatorname{Sin} \theta = \dfrac{{{\text{Opposit side}}}}{{{\text{Hypoyenuse}}}}\], then we have

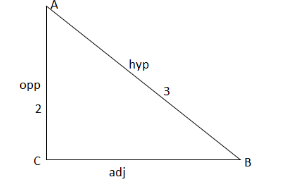
By Pythagoras theorem we have \[A{B^2} = A{C^2} + C{B^2}\]. Using thus we can find the adjacent side.
Substituting we have,
\[ \Rightarrow {3^2} = {2^2} + C{B^2}\]
Rearranging we have,
\[ \Rightarrow C{B^2} = 9 - 4\]
\[ \Rightarrow C{B^2} = 5\]
Taking square root on both sides,
\[ \Rightarrow CB = \sqrt 5 \].
We know that \[\tan \theta = \dfrac{{{\text{Opposit side}}}}{{{\text{Adjacent side}}}}\]
Then we have \[\tan \theta = \dfrac{2}{{\sqrt 5 }}\].
Let’s see the second method we know the identity formula, \[{\cos ^2}\theta + {\sin ^2}\theta = 1\].
Let’s consider \[ \Rightarrow \dfrac{1}{{{{\cos }^2}\theta }} = \dfrac{{{{\cos }^2}\theta + {{\sin }^2}\theta }}{{{{\cos }^2}\theta }}\]
Splitting in the right hand sides we have,
\[ \Rightarrow \dfrac{1}{{{{\cos }^2}\theta }} = \dfrac{{{{\cos }^2}\theta }}{{{{\cos }^2}\theta }} + \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }}\]
Cancelling cosine we have,
\[ \Rightarrow \dfrac{1}{{{{\cos }^2}\theta }} = 1 + \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }}\]
We know that \[\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}\], so we get
\[ \Rightarrow \dfrac{1}{{{{\cos }^2}\theta }} = 1 + {\tan ^2}\theta \]
\[ \Rightarrow 1 + {\tan ^2}\theta = \dfrac{1}{{{{\cos }^2}\theta }}\]
Subtracting 1 on both sides, we have:
\[ \Rightarrow {\tan ^2}\theta = \dfrac{1}{{{{\cos }^2}\theta }} - 1\]
Squaring on both sides,
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{1}{{{{\cos }^2}\theta }} - 1} \]
Using the identity formula \[{\cos ^2}\theta + {\sin ^2}\theta = 1\] we have \[{\cos ^2}\theta = 1 - {\sin ^2}\theta \].
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{1}{{1 - {{\sin }^2}\theta }} - 1} \]
We know that \[ \Rightarrow \sin \theta = \dfrac{2}{3}\], then we have:
\[ \Rightarrow \sin \theta = \dfrac{2}{3}\tan \theta = \sqrt {\dfrac{1}{{1 - {{\left( {\dfrac{2}{3}} \right)}^2}}} - 1} \]
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{1}{{1 - \left( {\dfrac{4}{9}} \right)}} - 1} \]
Taking L.C.M. we have,
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{1}{{\left( {\dfrac{{9 - 4}}{9}} \right)}} - 1} \]
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{1}{{\left( {\dfrac{5}{9}} \right)}} - 1} \]
Rearranging we have,
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{9}{5} - 1} \]
Again taking L.C.M. we have,
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{{9 - 5}}{5}} \]
\[ \Rightarrow \tan \theta = \sqrt {\dfrac{4}{5}} \]
We know the square root of 4 is 2.
\[ \Rightarrow \tan \theta = \dfrac{2}{{\sqrt 5 }}\]
In both the cases we have, \[\tan \theta = \dfrac{2}{{\sqrt 5 }}\].
But we have taken \[\theta = \arcsin \left( {\dfrac{2}{3}} \right)\] so we get,
\[\tan \left( {\arcsin \left( {\dfrac{2}{3}} \right)} \right) = \dfrac{2}{{\sqrt 5 }}\] is the required answer.
So, the correct answer is “ $ \dfrac{2}{{\sqrt 5 }} $ ”.

Note: As we can see that in above we have done in two methods. In both methods we have the same answer. Choose method one which is easy to do. We know that ‘arcsin’ is an inverse trigonometry of sine function. The above can see that when taking the sine on both sides arcsin and sine will cancel out. Careful in the calculation part. We know \[{\sin ^2}\theta = {(\sin \theta )^2}\].