Question

How do you evaluate $\sin \left( {\dfrac{\pi }{2}} \right)$?

Answer 1

Hint: Before evaluating the values of trigonometric functions we must be familiar with the concept of unit circle. The unit circle is a circle of unit radius that is its radius is $1$ . It is centered at the origin of the Cartesian coordinate system and we use the unit circle to identify the values of the standard trigonometric functions as the angle $\theta $ varies between ${0^0}{\text{ to 36}}{{\text{0}}^0}{\text{ }}\left( {0{\text{ to 2}}\pi {\text{ radians}}} \right)$ .

Complete step by step solution:
The unit circle in the Cartesian plane is shown below:

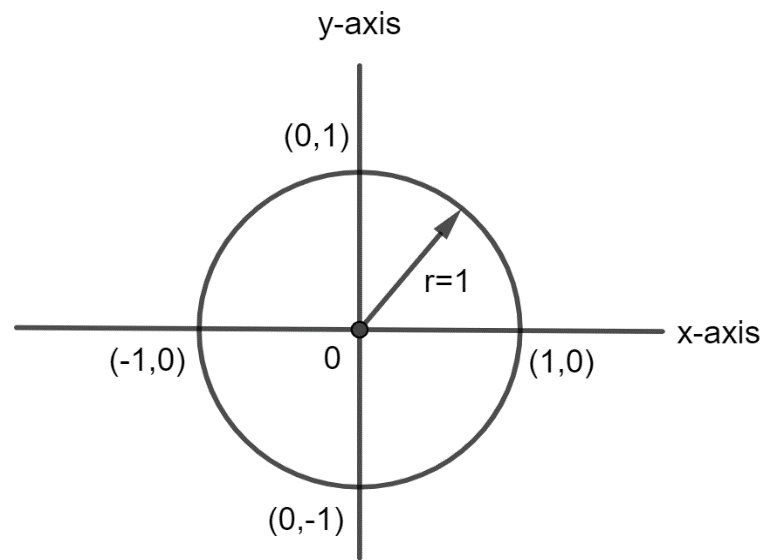
Figure $\left( 1 \right)$ : The unit circle
We know that for any right -angled triangle, sine function is defined as the ratio of length of perpendicular side to the length of the hypotenuse side i.e. $\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$ .
Let us draw a right angle triangle within the unit circle which is shown below in figure $\left( 2 \right)$ ;
In the right angle triangle OBA ; the value of sine function can be defined as ;
$ \Rightarrow \sin \theta = \dfrac{{{\text{AB}}}}{{{\text{OB}}}} = {\text{AB }}\left( {\because {\text{OB = r = 1}}} \right)$
$\therefore \sin \theta = {\text{AB }}......\left( 1 \right)$
Similarly, we can calculate the value of cosine function, we know that for right-angled triangle the cosine function is defined as the ratio of length of adjacent side to the length of the hypotenuse side i.e. $\cos \theta = \dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$ . In the right angle triangle OBA ; the value of cosine function can be defined as;
$ \Rightarrow \cos \theta = \dfrac{{{\text{OA}}}}{{{\text{OB}}}} = {\text{OA }}\left( {\because {\text{OB = r = 1}}} \right)$
$\therefore \cos \theta = {\text{OA }}......\left( 2 \right)$
From the above equations, it can be concluded that the vertical axis i.e. y-axis in the Cartesian plane can be represented as $\sin \theta $ and the horizontal axis i.e. the x-axis can be represented as $\cos \theta $ . Therefore the coordinates $\left( {x,y} \right)$ become $\left( {\cos \theta ,\sin \theta } \right)$ .

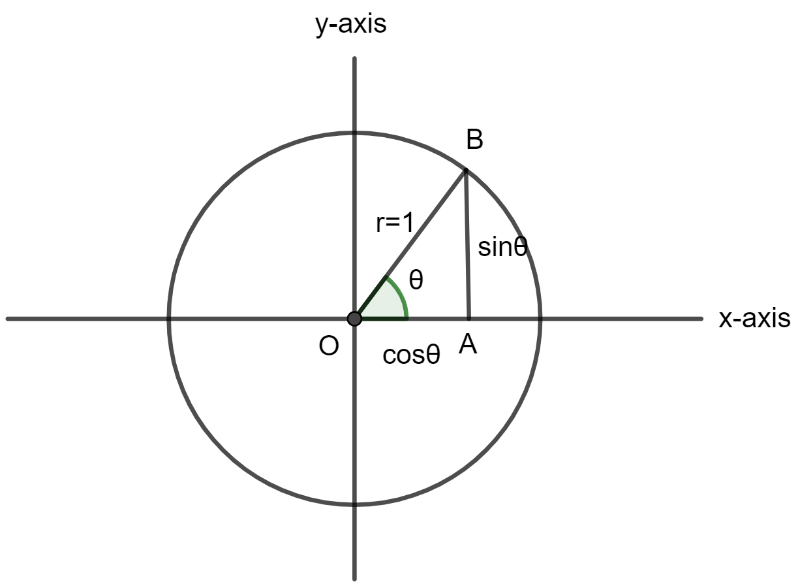
Figure $\left( 2 \right)$ : The right-angled triangle inside the unit circle
According to the question, we have to calculate the value of $\sin \left( {\dfrac{\pi }{2}} \right)$ ;
From figure $\left( 3 \right)$ , as we increase the value of angle $\theta $ the magnitude of opposite (perpendicular) side will increase and the magnitude of adjacent side (base) will decrease. When the value of $\theta $ becomes $\dfrac{\pi }{2}{\text{ i}}{\text{.e}}{\text{. 9}}{{\text{0}}^0}$ , the adjacent side will get vanished and the opposite side of the right-angled triangle will coincide with the hypotenuse side. This means that ;
$ \Rightarrow {\text{Opposite side = Hypotenuse side}}$
From the definition of sine function, we know that;
$ \Rightarrow \sin \left( {\dfrac{\pi }{2}} \right) = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = 1$ ( as both becomes equal at $\theta = \dfrac{\pi }{2}$ )
Hence, $\sin \theta = \sin \left( {\dfrac{\pi }{2}} \right) = 1$ .
Therefore, the value of $\sin \left( {\dfrac{\pi }{2}} \right)$ is $1$ .

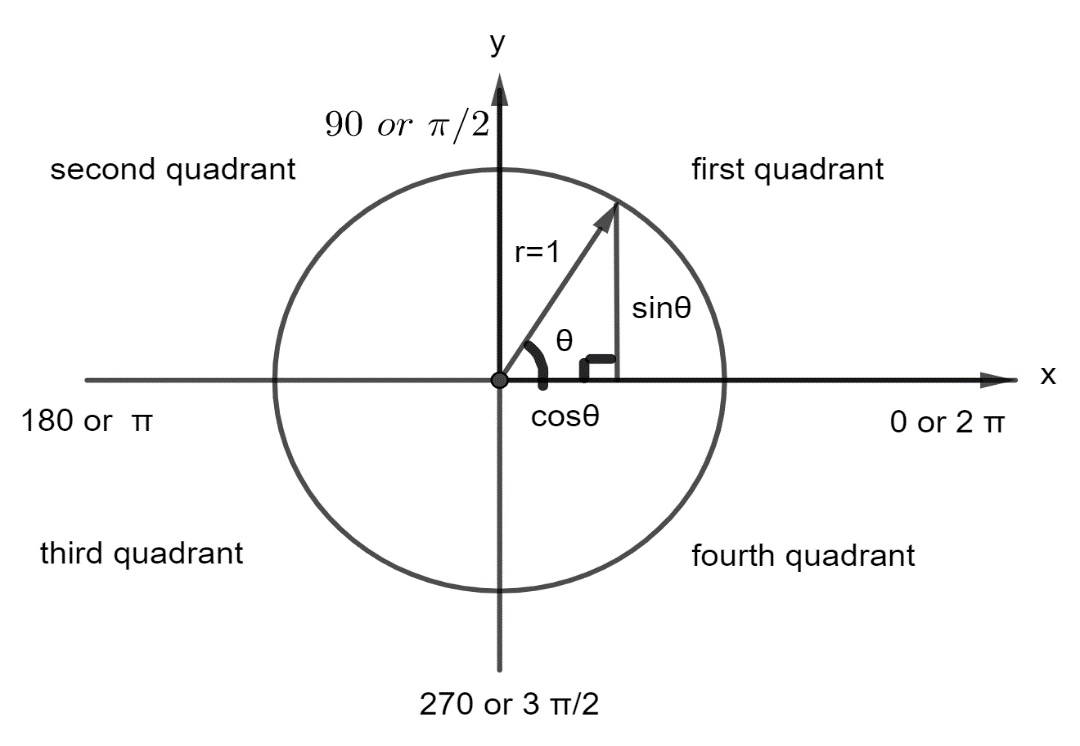
Figure $\left( 3 \right)$ : The quadrant system

Note:
Using the quadrant system shown in figure $\left( 3 \right)$ , we can calculate any value for the functions. Notice that other trigonometric function’s values can be easily derived from sine and cosine function values. Some of the important results for sine and cosine values are: $\left( 1 \right)\sin {0^0},\sin \pi ,\sin 2\pi ,\sin 3\pi ,.... = 0$ . $\left( 2 \right)\sin \dfrac{\pi }{2},\sin \dfrac{{5\pi }}{2},\sin \dfrac{{9\pi }}{2},....... = 1$ .$\left( 3 \right)\sin \dfrac{{3\pi }}{2},\sin \dfrac{{7\pi }}{2},\sin \dfrac{{11\pi }}{2},...... = - 1$ . $\left( 4 \right)\cos \dfrac{\pi }{2},\cos \dfrac{{3\pi }}{2},\cos \dfrac{{5\pi }}{2},\cos \dfrac{{7\pi }}{2},........ = 0$ .$\left( 5 \right)\cos {0^0},\cos 2\pi ,\cos 4\pi ,...... = 1$ . $\left( 6 \right)\cos \pi ,\cos 3\pi ,\cos 5\pi ,....... = - 1$.