Question

How do you evaluate $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ ?

Answer 1

Hint: We first find the principal value of x for which $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ . In that domain, equal value of the same ratio gives equal angles. We find the angle value for x. At the end we also find the general solution for the equation $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ .

Complete step-by-step answer:
It’s given that $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ . The value in fraction is $ \dfrac{\sqrt{2}}{2} $ . This is equal to $ \dfrac{1}{\sqrt{2}} $ .
We need to find x for which $ {{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right) $ .
We know that in the principal domain or the periodic value of
$ -\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2} $ for $ \sin x $ , if we get $ \sin a=\sin b $ where $ -\dfrac{\pi }{2}\le a,b\le \dfrac{\pi }{2} $ then $ a=b $ .
We have the value of $ \sin \left( \dfrac{\pi }{4} \right) $ as $ \dfrac{1}{\sqrt{2}} $ . $ -\dfrac{\pi }{2}<\dfrac{\pi }{4}<\dfrac{\pi }{2} $ .
Therefore, $ \sin \left( x \right)=\dfrac{1}{\sqrt{2}}=\sin \left( \dfrac{\pi }{4} \right) $ which gives $ x=\dfrac{\pi }{4} $ .
For $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ , the value of x is $ x=\dfrac{\pi }{4} $ .
We also can show the solutions (primary and general) of the equation $ \sin \left( x \right)=\dfrac{1}{\sqrt{2}} $ through the graph. We take $ y=\sin \left( x \right)=\dfrac{1}{\sqrt{2}} $ . We got two equations $ y=\sin \left( x \right) $ and $ y=\dfrac{1}{\sqrt{2}} $ . We place them on the graph and find the solutions as their intersecting points.

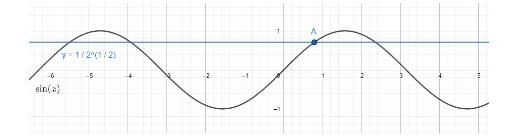
We can see the primary solution in the interval $ -\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2} $ is the point A as $ x=\dfrac{\pi }{4} $ .
All the other intersecting points of the curve and the line are general solutions.
So, the correct answer is “ $ x=\dfrac{\pi }{4} $ ”.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $ -\infty \le x\le \infty $ . In that case we have to use the formula $ x=n\pi +{{\left( -1 \right)}^{n}}a $ for $ \sin \left( x \right)=\sin a $ where $ -\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2} $ . For our given problem $ {{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right) $ , the general solution will be $ x=n\pi +{{\left( -1 \right)}^{n}}\dfrac{\pi }{4} $ . Here $ n\in \mathbb{Z} $ .