Question

How do you evaluate \[\sec \left( {{\tan }^{-1}}8 \right)\] without a calculator?

Answer 1

Hint: We explain the function $\arctan \left( x \right)$. We express the inverse function of tan in the form of $\arctan \left( x \right)={{\tan }^{-1}}x$. We draw the graph of $\arctan \left( x \right)$ and the line $x=8$ to find the intersection point. Thereafter we take the sec ratio of that angle to find the solution. We also use the representation of a right-angle triangle with height and base ratio being 8 and the angle being $\theta $.

Complete step-by-step solution:
The internal part \[{{\tan }^{-1}}8\] of \[\sec \left( {{\tan }^{-1}}8 \right)\] is an angle. We assume \[{{\tan }^{-1}}8=\theta \].
This gives in ratio \[\tan \theta =8\]. We know \[\tan \theta =\dfrac{\text{height}}{\text{base}}\].
We can take the representation of a right-angle triangle with height and base ratio being 8 and the angle being $\theta $. The height and base were considered with respect to that particular angle $\theta $.

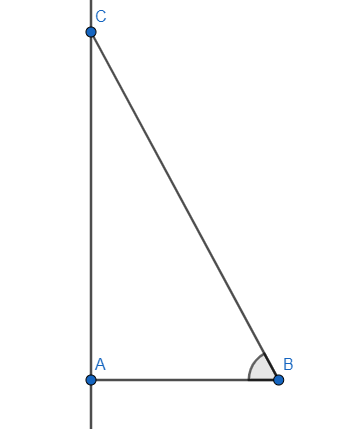
In this case we take $AB=x$ and keeping the ratio in mind we have $AC=8x$ as the ratio has to be 8.
Now we apply the Pythagoras’ theorem to find the length of BC. $B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}$.
So, $B{{C}^{2}}={{x}^{2}}+{{\left( 8x \right)}^{2}}=65{{x}^{2}}$ which gives $BC=\sqrt{65}x$.
We need to find \[\sec \left( {{\tan }^{-1}}8 \right)\] which is equal to \[\sec \theta \].
This ratio gives \[\sec \theta =\dfrac{\text{hypotenuse}}{\text{base}}\]. So, \[\sec \theta =\dfrac{BC}{AB}=\dfrac{\sqrt{65}x}{x}=\sqrt{65}\].
Therefore, \[\sec \left( {{\tan }^{-1}}8 \right)\] is equal to \[\sqrt{65}\].

Note: We can also apply the trigonometric image form to get the value of \[\sec \left( {{\tan }^{-1}}8 \right)\].
It’s given that \[\tan \theta =8\] and we need to find \[\sec \theta \]. We know $\sec \theta =\sqrt{1+{{\tan }^{2}}\theta }$.
Putting the values, we get $\sec \theta =\sqrt{1+{{\tan }^{2}}\theta }=\sqrt{1+{{8}^{2}}}=\sqrt{65}$.