
How do you evaluate $\left( _{7}^{8} \right)$ using Pascal's triangle?
Answer
547.8k+ views
Hint: To evaluate the above form $\left( _{7}^{8} \right)$ we should know the basics about Pascal's triangle. In mathematics, it is a triangular array of the binomial coefficients that arises in the algebra probability theory and many more. Whenever I have sum of the sort $\left( _{k}^{n} \right)$ where the number $n$ corresponds to the row number of Pascal's triangle and $k$ corresponds to the column number of that row, where the first column has the value of$k=0$. Here $\left( _{k}^{n} \right)$is typically read as $''n$ choose$k''$. There is a formula to find $\left( _{k}^{n} \right)$which is
$\Rightarrow \left( _{k}^{n} \right)=\dfrac{n!}{k!\left( n-1 \right)!}$ Where! is the factorial function.
Complete step by step solution:
The given equation $\left( _{7}^{8} \right)$ .now compare this with the $\left( _{k}^{n} \right)=\dfrac{n!}{k!\left( n-1 \right)!}$ we get $n=8$ and $k=7$.
Now putting the values for $n$and $k$in this situation gives:
$\begin{align}
& \Rightarrow \left( _{k=7}^{n=8} \right)=\left( \dfrac{\left( n=8 \right)!}{\left( k=7 \right)!\left( 8-7 \right)!} \right) \\
& \Rightarrow \left( _{7}^{8} \right)=\dfrac{8!}{7!\left( 8-7 \right)!} \\
& \Rightarrow \left( _{7}^{8} \right)=\dfrac{8\cdot 7!}{7!\cdot 1!} \\
& \Rightarrow \left( _{7}^{8} \right)=8 \\
\end{align}$
Hence the solution of $\left( _{7}^{8} \right)$ is $8$.
We can also Pascal's triangle which is constructed as; Pascal's triangle is a never ending equilateral triangle of numbers that follows a rule of adding the two numbers above to get the number below. Two of the sides are “all 1`s” and because the triangle is infinite, there is no “bottom side”.
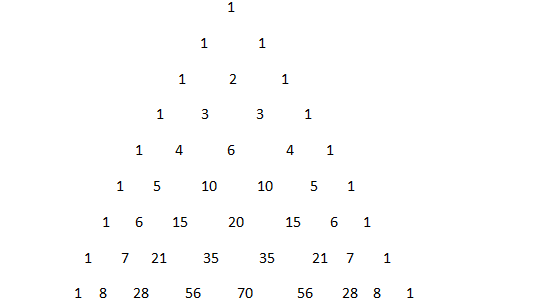
So here in the bottom row we can find our required term as 8.
Note: To solve these types of questions there is also another method. If we have $\left( _{n-1}^{n} \right)$ then by using the formula, the solution becomes\[\left( _{n-1}^{n} \right)=n\]. Remember the first row and first column are given by $n=0$ and $k=0$ respectively.
$\Rightarrow \left( _{k}^{n} \right)=\dfrac{n!}{k!\left( n-1 \right)!}$ Where! is the factorial function.
Complete step by step solution:
The given equation $\left( _{7}^{8} \right)$ .now compare this with the $\left( _{k}^{n} \right)=\dfrac{n!}{k!\left( n-1 \right)!}$ we get $n=8$ and $k=7$.
Now putting the values for $n$and $k$in this situation gives:
$\begin{align}
& \Rightarrow \left( _{k=7}^{n=8} \right)=\left( \dfrac{\left( n=8 \right)!}{\left( k=7 \right)!\left( 8-7 \right)!} \right) \\
& \Rightarrow \left( _{7}^{8} \right)=\dfrac{8!}{7!\left( 8-7 \right)!} \\
& \Rightarrow \left( _{7}^{8} \right)=\dfrac{8\cdot 7!}{7!\cdot 1!} \\
& \Rightarrow \left( _{7}^{8} \right)=8 \\
\end{align}$
Hence the solution of $\left( _{7}^{8} \right)$ is $8$.
We can also Pascal's triangle which is constructed as; Pascal's triangle is a never ending equilateral triangle of numbers that follows a rule of adding the two numbers above to get the number below. Two of the sides are “all 1`s” and because the triangle is infinite, there is no “bottom side”.
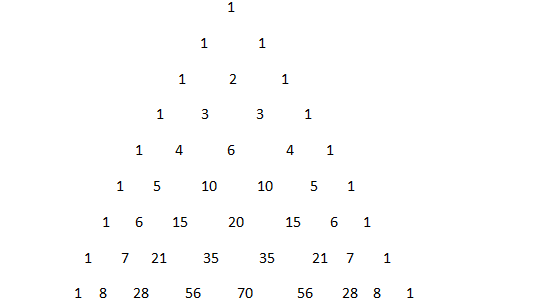
So here in the bottom row we can find our required term as 8.
Note: To solve these types of questions there is also another method. If we have $\left( _{n-1}^{n} \right)$ then by using the formula, the solution becomes\[\left( _{n-1}^{n} \right)=n\]. Remember the first row and first column are given by $n=0$ and $k=0$ respectively.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




