Question

Evaluate following trigonometric ratios: \[\]
(i) $\dfrac{\sin {{18}^{\circ }}}{\cos {{72}^{\circ }}}$ \[\]
(ii) $\dfrac{\tan {{26}^{\circ }}}{\tan {{74}^{\circ }}}$\[\]
(iii) $\cos {{48}^{\circ }}-\sin {{72}^{\circ }}$\[\]
(iv) $\operatorname{cosec}{{31}^{\circ }}-\sec {{59}^{\circ }}$\[\]

Answer 1

Hint: We recall the definition of six trigonometric ratios and find the reduction formula where an angle is reflected about the angle vector of ${{45}^{\circ }}$ to get the complementary angle. If the two complementary angles are $\theta ,{{90}^{\circ }}-\theta $ then the reduction formula are given by $\sin \theta =\cos \left( {{90}^{\circ }}-\theta \right)$, $\tan \theta =\cot \left( {{90}^{\circ }}-\theta \right)$ and $\operatorname{cosec}\theta =\sec \left( {{90}^{\circ }}-\theta \right)$. We take the smaller angle in the questions as $\theta $ and use reduction formula.\[\]

Complete step-by-step solution:

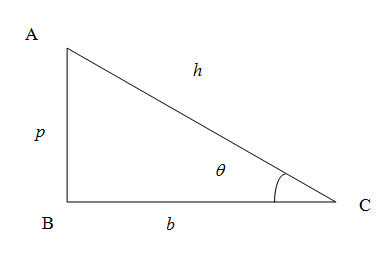
We know that in a right-angled triangle (Here ABC) the side opposite to the right angle (Here $\angle ABC$) is called hypotenuse (here AC) denoted as $h$, the vertical side AB is called perpendicular denoted as $p$ and the horizontal side BC is called the base denoted as $b$.
We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse. In the figure the sine of the angle $\angle ACB=\theta $ is given by
\[\sin \theta =\dfrac{AB}{AC}=\dfrac{p}{h}\]
Similarly the cosine of an angle is the ratio of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle $\theta $
\[\cos \theta =\dfrac{BC}{AC}=\dfrac{b}{h}\]
The tangent of the angle is the ratio of opposite side to the adjacent side (excluding hypotenuse) . So we have tangent of the angle of angle $\theta $
\[\tan \theta =\dfrac{AB}{BC}=\dfrac{p}{b}\]
The reciprocals of sine, cosine and tangent of angle are defined as cosecant, secant and cotangent of the angle which means,
\[\operatorname{cosec}\theta =\dfrac{1}{\sin \theta },\sec \theta =\dfrac{1}{\cos \theta },\cot \theta =\dfrac{1}{\tan \theta }\]
 Let us consider the right angled triangle ABC. We have,
\[\begin{align}
  & A+B+C={{180}^{\circ }} \\
 & \Rightarrow A+C={{180}^{\circ }}-{{90}^{\circ }}=90{}^{\circ } \\
 & \Rightarrow A={{90}^{\circ }}-C \\
\end{align}\]
We have taken$\angle ACB=C=\theta $. So we have
\[C=\theta ,A={{90}^{\circ }}-\theta \]
Let us take sine and cosines of angle $C=\theta ,A={{90}^{\circ }}-\theta $.
\[\begin{align}
  & \sin \theta =\dfrac{p}{h},\sin \left( {{90}^{\circ }}-\theta \right)=\dfrac{BC}{AC}=\dfrac{b}{h} \\
 & \cos \theta =\dfrac{b}{h},\cos \left( {{90}^{\circ }}-\theta \right)=\dfrac{AB}{AC}=\dfrac{p}{h} \\
\end{align}\]
We conclude from above that
\[\sin \theta =\cos \left( {{90}^{\circ }}-\theta \right),\cos \theta =\sin \left( {{90}^{\circ }}-\theta \right)\]
The above identity is called reflection identity also known as reduction formula which reflects complementary trigonometric ratio about an angle vector of ${{45}^{\circ }}$. We can similarly derive the reduction formula for tangent and co-tangent or secant and cosecant as
\[\begin{align}
  & \tan \theta =\cot \left( {{90}^{\circ }}-\theta \right),\cot \theta =\tan \left( {{90}^{\circ }}-\theta \right) \\
 & \operatorname{cosec}\theta =\sec \left( {{90}^{\circ }}-\theta \right),\sec \theta =\text{cosec}\left( {{90}^{\circ }}-\theta \right) \\
\end{align}\]
Let us now use reduction formulae to solve the question.
(i) We are asked to evaluate the trigonometric expression $\dfrac{\sin {{18}^{\circ }}}{\cos {{72}^{\circ }}}$. Let us take $\theta ={{18}^{\circ }}$and then we have $90{}^{\circ }-\theta ={{90}^{\circ }}-{{18}^{\circ }}={{72}^{\circ }}$. So we use the reduction formula of sine-cosine for complementary angles ${{18}^{\circ }},{{72}^{\circ }}$ to have.
 \[\dfrac{\sin {{18}^{\circ }}}{\cos {{72}^{\circ }}}=\dfrac{\sin {{18}^{\circ }}}{\cos \left( {{90}^{\circ }}-{{18}^{\circ }} \right)}=\dfrac{\sin {{18}^{\circ }}}{\sin {{18}^{\circ }}}=1\]
(ii) We are asked to evaluate the trigonometric expression$\dfrac{\tan {{26}^{\circ }}}{\cot {{64}^{\circ }}}$. Let us take $\theta ={{26}^{\circ }}$and then we have$90{}^{\circ }-\theta ={{90}^{\circ }}-{{26}^{\circ }}={{64}^{\circ }}$. So we use the reduction formula of tangent -cotangent for complementary angles ${{26}^{\circ }},{{64}^{\circ }}$ to have.
\[\dfrac{\tan {{26}^{\circ }}}{\cot {{64}^{\circ }}}=\dfrac{\tan {{26}^{\circ }}}{\cot \left( {{90}^{\circ }}-{{26}^{\circ }} \right)}=\dfrac{\tan {{26}^{\circ }}}{\tan {{26}^{\circ }}}=1\]
(iii) We are asked to evaluate the trigonometric expression $\cos {{48}^{\circ }}-\sin {{42}^{\circ }}$. Let us take $\theta ={{42}^{\circ }}$and then we have $90{}^{\circ }-\theta ={{90}^{\circ }}-{{42}^{\circ }}={{48}^{\circ }}$. So we use the reduction formula of sine-cosine for complementary angles ${{48}^{\circ }},{{42}^{\circ }}$ to have.
\[\cos {{48}^{\circ }}-\sin 42=\cos {{48}^{\circ }}-\sin {{\left( 90-48 \right)}^{\circ }}=\cos {{48}^{\circ }}-\cos {{48}^{\circ }}=0\]
(iv) We are asked to evaluate the trigonometric expression $\operatorname{cosec}{{31}^{\circ }}-\sec {{59}^{\circ }}$. Let us take $\theta ={{31}^{\circ }}$and then we have $90{}^{\circ }-\theta ={{90}^{\circ }}-{{31}^{\circ }}={{59}^{\circ }}$. So we use the reduction formula of secant-cosecant for complementary angles ${{31}^{\circ }},{{59}^{\circ }}$ to have
\[\operatorname{cosec}{{31}^{\circ }}-\cot {{59}^{\circ }}=\operatorname{cosec}{{31}^{\circ }}-\cot {{\left( 90-59 \right)}^{\circ }}=\operatorname{cosec}{{31}^{\circ }}-\operatorname{cosec}{{31}^{\circ }}=0\]

Note: We note that we have solved from taking the smaller of complementary angles as $\theta ={{18}^{\circ }},{{26}^{\circ }},{{42}^{\circ }},{{31}^{\circ }}$ and we can also solve taking the larger of complementary angles as$\theta ={{72}^{\circ }},{{64}^{\circ }},{{48}^{\circ }},{{59}^{\circ }}$. If an angle is reflected by the angle vector of ${{90}^{\circ }}$ then we will get its supplementary angle then we will have $\sin \left( {{180}^{\circ }}-\theta \right)=\sin \theta ,\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $ and $\tan \left( {{180}^{\circ }}-\theta \right)=-\tan \theta $.