Question

How do you evaluate $\cos \left( \dfrac{3\pi }{2}-x \right)$ ?

Answer 1

Hint: Try to expand $\cos \left( \dfrac{3\pi }{2}-x \right)$ and express it in the values that we already know the sin and cos. Then use the trigonometric identity $\cos (a-b)=\cos a\cos b+\sin a\sin b$ . Here, a is $\dfrac{3\pi }{2}$ and b is $x$ .

Complete step by step answer:
This type of question is mainly asked to check whether one remembers the formula $\cos (a-b)=\cos a\cos b+\sin a\sin b$ and the values of sin and cos at $\dfrac{3\pi }{2}$ .
We know, $\sin \left( \dfrac{(4n+3)\pi }{2} \right)$ is -1 for all n belonging to integers, $\cos \left( \dfrac{\left( 2n+1 \right)\pi }{2} \right)$ is 0 for all n belonging to integers.
Now, taking a as $\dfrac{3\pi }{2}$ and b as $x$ and applying it in the formula of $\cos (a-b)=\cos a\cos b+\sin a\sin b$ we have,
$\Rightarrow \cos \left( \dfrac{3\pi }{2}-x \right)=\cos \left( \dfrac{3\pi }{2} \right)\cos x+\sin \left( \dfrac{3\pi }{2} \right)\sin x$
$\sin \left( \dfrac{3\pi }{2} \right)$ is of the form $\sin \left( \dfrac{(4n+3)\pi }{2} \right)$ so equal to -1 and$\cos \left( \dfrac{3\pi }{2} \right)$ is of the form $\cos \left( \dfrac{\left( 2n+1 \right)\pi }{2} \right)$ so equal to 0.
$\Rightarrow \cos \left( \dfrac{3\pi }{2} \right)\cos x+\sin \left( \dfrac{3\pi }{2} \right)\sin x=0\times \cos x+\left( -1 \right)\times \sin x$

Thus, $\cos \left( \dfrac{3\pi }{2}-x \right)=-\sin x$

Note: One must remember the basic values of sin and cos, it is very common to make mistakes in the signs for +1 and -1 when using the values of sin and cos. Another common mistake is to make sign mistakes in the \[\cos \left( a-b \right)\] formula.

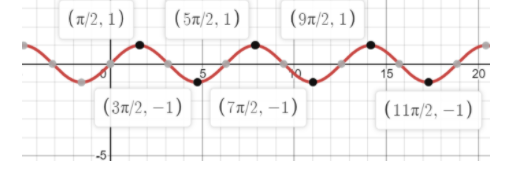
Alternatively, one can do this in two steps. First, see from the graph that $\cos \left( \pi -a \right)=-\cos a$ so $\Rightarrow \cos \left( \dfrac{3\pi }{2}-x \right)=\cos \left( \pi -\left( -\dfrac{\pi }{2}+x \right) \right)$ and then we use that $\cos \left( -a \right)=\cos a$ and $\cos \left( \dfrac{\pi }{2}-x \right)=\sin x$ . So, $\Rightarrow \cos \left( \pi -\left( -\dfrac{\pi }{2}+x \right) \right)=-\cos \left( x-\dfrac{\pi }{2} \right)=\cos \left( \dfrac{\pi }{2}-x \right)=\sin \left( x \right)$ . You can use the following to remember some of the above:
In the first quadrant, all the basic three trigonometric functions are positive. In the second quadrant, only sin is positive. In the third only tan is negative, and in the fourth only cos is negative.