Question

How do you evaluate $\arctan (\dfrac{1}{{\sqrt 3 }})$?

Answer 1

Hint: The arctangent is the inverse of the trigonometric representation of tangent (Tan). The range of arctangent is from negative of $\dfrac{\pi }{2}$ to positive of $\dfrac{\pi }{2}$. The domain of arctangent is from negative infinity to positive infinity. It is a bijective function, which means it will be invertible. This property will be very useful in this question.

Complete step by step solution:
According to the question, we have to find the value of $\arctan (\dfrac{1}{{\sqrt 3 }})$,
Let $\arctan (\dfrac{1}{{\sqrt 3 }})$ = x (variable)
So $\dfrac{1}{{\sqrt 3 }} = $ $\tan x$ (Taking tan both sides)
Now,
Let us draw a triangle with $\tan x$= $\dfrac{1}{{\sqrt 3 }}$
In this right angled triangle,
Base = $\sqrt 3 $
Height = 1
Hypotenuse = 2

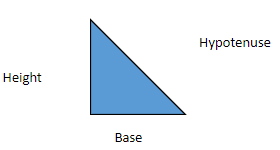
So the angle between the base and the height = 90°
And the angle between the base and the hypotenuse = the required angle
So, as we know the value of $\tan \theta $ for different values of $\theta $, we know that when $\theta $ = 30° $\tan \theta $ will give the value $\dfrac{1}{{\sqrt 3 }}$
And, as we know that 30° = $\dfrac{\pi }{6}$
Now,
$\tan x$=$\dfrac{1}{{\sqrt 3 }}$ , and x = $\dfrac{\pi }{6}$
$x$=$\arctan (\dfrac{1}{{\sqrt 3 }})$ = $\dfrac{\pi }{6}$

Therefore, our answer is $ x = \dfrac{\pi }{6}$

Note:
The arctangent is the inverse of the tan trigonometric function. It is a bijective function, that is, it gives a unique value of every unique input and for every output one single input is considered. Bijective also means it is invertible, that is why we changed arctan to tan easily in our solution. This property is valid for every input, unlike in other inverse trigonometric functions where there is a limitation in their respective domain.