Question

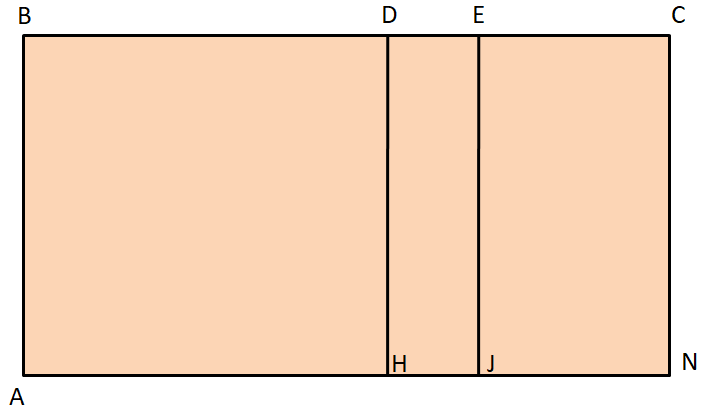
Euclid showed geometrically the distributive law of multiplication. Let $\overline{AB}$ and $\overline{BC}$ be two straight lines, tracing a rectangle and let $\overline{BC}$ be cut at random points D and E. Use this fact to show the distributive law?

Answer 1

Hint: The distributive law from the given figure can be proved by relating the area of the different rectangles. Firstly, we have to assume $AB=a$, $BD=b$, $DE=c$, and $EC=d$. Then using the properties of the rectangles, we can obtain the lengths of the other sides also. From these values, we can obtain the areas of the rectangles ABCN, ABDH, DEJH, and ECNJ. From the given figure, the area of the rectangle ABCN is equal to the sum of the areas of the rectangles ABDH, DEJH, and ECNJ. On writing this as a mathematical statement, and on substituting the values of the areas, we will get the statement of the distributive law.

Complete step-by-step solution:
Let us assume $AB=a$. Also, let us assume that $BD=b$, $DE=c$ and $EC=d$.
From the given figure, we can see that the points D and E lie on the side BC. Therefore, we can write
$\Rightarrow BC=BD+DE+EC$
On putting $BD=b$, $DE=c$ and $EC=d$ in the above equation, we get
$\Rightarrow BC=b+c+d.......\left( i \right)$
From the given figure, we can see that the sides AB, DH, EJ and CN are parallel to each other. Therefore, using the properties of a parallelogram, we can say that
$\Rightarrow DH=EJ=DN=AB=a......\left( ii \right)$
Now, from the above figure we can write the area of the rectangle ABCN as
$\Rightarrow ar\left( ABCN \right)=AB\times BC$
On putting $AB=a$ and the equation (i) in the above equation, we get
$\Rightarrow ar\left( ABCN \right)=a\left( b+c+d \right).........\left( iii \right)$
Now, considering the rectangle ABDH, we can write its area as
$\Rightarrow ar\left( ABDH \right)=AB\times BD$
On putting $AB=a$ and $BD=b$ in the above equation, we get
$\Rightarrow ar\left( ABDH \right)=ab.......\left( iv \right)$
Similarly, we can write the area of the rectangle DEJH as
$\Rightarrow ar\left( DEJH \right)=DH\times DE$
On putting $DE=c$ and from the equation (ii) $DH=a$ we get
$\Rightarrow ar\left( DEJH \right)=ac.......\left( v \right)$
Finally, the area of the rectangle ECNJ is given by
$\Rightarrow ar\left( ECNJ \right)=EJ\times EC$
Putting $EC=d$ and from (ii) $EJ=a$ we get
$\Rightarrow ar\left( ECNJ \right)=ad.......\left( vi \right)$
Now, from the given figure we can also observe that the area of the rectangle ABCN is equal to the sum of the areas of the rectangles ABDH, DEJH, and ECNJ, which means we can write
$\Rightarrow ar\left( ABCN \right)=ar\left( ABDH \right)+ar\left( DEJH \right)+ar\left( ECNJ \right)$
On putting the equations (iii), (iv), (v), and (vi) we get
$\Rightarrow a\left( b+c+d \right)=ab+ac+ad$
Hence, we have proved the distributive law.

Note: We can also prove the distributive law by relating the areas of the rectangles ABDH, DEJH, and ABEJ by following the same process as in the above solution. Using these rectangles, we will obtain the distributive law as $a\left( b+c \right)=ab+ac$.