Question

How do you estimate the volume of a silo with diameter 11.1 feet and height 20 feet? \[\]

Answer 1

Hint: We recall the shape of silo which has a cylindrical part and a hemi-spherical part at one end. We find the volume of the silo as the sums of volume of the cylinder ${{V}_{c}}=\pi {{r}^{2}}h$ and the volume of hemi-sphere $\dfrac{2}{3}\pi {{r}^{3}}$ where $h$ is the height and $r$ is the radius of the cylinder. \[\]

Complete step-by-step solution:
We know that silos are containers cylindrical in shape which has one end at the top in a hemi-spherical shape. So the volume of the cylinder with radius at the base $r$ and height $h$ is given by
\[{{V}_{c}}=\pi {{r}^{2}}h\]
We know that the volume of a hemi-sphere is half the volume of a sphere. The radius at the top base of the cylindrical part is also the radius of the hemi-sphere. So the volume of the hemisphere with radius $r$ is
\[{{V}_{h}}=\dfrac{2}{3}\pi {{r}^{3}}\]
So the required volume of the silos is
\[V={{V}_{c}}+{{V}_{h}}=\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}\]
We are given in the question the diameter not the radius. Let us use the fact that radius $r$ is always half the diameter $d$ that is $r=\dfrac{d}{2}$and have the formula for volume of silos as
\[V={{V}_{c}}+{{V}_{h}}=\pi {{\left( \dfrac{d}{2} \right)}^{2}}h+\dfrac{2}{3}\pi {{\left( \dfrac{d}{2} \right)}^{3}}\]

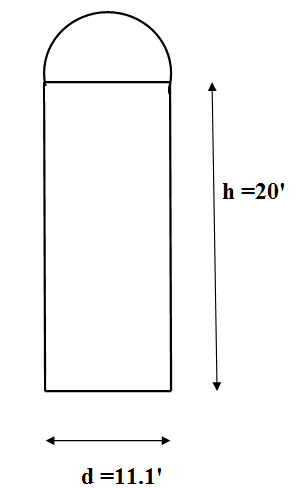
We are given the question that the diameter of the silos is $d=11.1$ feet and height $h=20$ feet. Since we are asked to estimate not exactly calculate so we approximate $d=11.1\approx 10$ feet and find the volume as
\[\begin{align}
  & V={{V}_{c}}+{{V}_{h}}=\pi {{\left( \dfrac{10}{2} \right)}^{2}}20+\dfrac{2}{3}\pi {{\left( \dfrac{10}{2} \right)}^{3}} \\
 & \Rightarrow V=\pi \times 25\times 20+\dfrac{2}{3}\pi \times 125 \\
 & \Rightarrow V=\pi \times 25\times 20+\dfrac{2}{3}\pi \times 125 \\
\end{align}\]
We use the approximated value $\pi \approx 3$ in the above step to have
\[\begin{align}
  & \Rightarrow V=3\times 25\times 20+\dfrac{2}{3}\times 3\times 125 \\
 & \Rightarrow V=1500+250 \\
 & \Rightarrow V=1750 \\
\end{align}\]
We have estimated the volume of the silo as 1750 cubic feet.

Note: We can also find the nearly exact volume of the silos by taking $d=11.1$ and $\pi =3.14$ and putting in the formula $V={{V}_{c}}+{{V}_{h}}=\pi {{\left( \dfrac{d}{2} \right)}^{2}}h+\dfrac{2}{3}\pi {{\left( \dfrac{d}{2} \right)}^{3}}$ to have the volume as $2291.89$ cubic unit. We note that silos are used as container structure for bulk storage of coal, grain , comment etc.