Question

How do you estimate the area under the graph of $f\left( x \right)=25-{{x}^{2}}$ from $x=0$ to $x=5$ using five approximating rectangles and right endpoints?

Answer 1

Hint: In this question we will first calculate the value of $\Delta x$ and then we will write all the endpoints of the equation and consider the right endpoints since it is mentioned in the question for us to use. We will then calculate the area of the rectangles and then add all the areas of the rectangles to get the estimated value of the area under the graph.

Complete step by step solution:
We have $f(x)=25-{{x}^{2}}$ for which we have to approximate area from $x=0$ to $x=5$ therefore we can say that $a=0$ and $b=5$
We know that $\Delta x=\dfrac{b-a}{n}$.
Since there are total $5$ intervals, $n=5$. On substituting all the values, we get:
$\Rightarrow \Delta x=\dfrac{5-0}{5}$
On simplifying, we get:
$\Rightarrow \Delta x=1$
Therefore, $\Delta x$ is the base of all the rectangles and the distance between all the endpoints.
now the left-most endpoint is $a$ and the next end point can be calculated by adding the previous end-point and $\Delta x$
therefore, we have the second end-point as $a+\Delta x$ which is $0+1=1$
now the next end-point will be $1+1=2$
similarly, all the endpoints are:
$\Rightarrow 0,1,2,3,4,5$
Now the right endpoints are:
$\Rightarrow 1,2,3,4,5$
Now to find the height at these endpoints, we will substitute their values in $f\left( x \right)=25-{{x}^{2}}$.
$\Rightarrow f\left( 1 \right)=24$
$\Rightarrow f\left( 2 \right)=21$
$\Rightarrow f\left( 3 \right)=16$
$\Rightarrow f\left( 4 \right)=9$
$\Rightarrow f\left( 5 \right)=0$
Now since $\Delta x$ is the base, the are would be the heights multiplied by the bases therefore the areas of the rectangles are:
$\Rightarrow 24\times 1=24$
$\Rightarrow 21\times 1=21$
$\Rightarrow 16\times 1=16$
$\Rightarrow 9\times 1=9$
$\Rightarrow 0\times 1=0$
Now the total area would be the areas of all the rectangles added therefore, we get:
$\Rightarrow 24+16+16+9+1$
On simplifying, we get:
$\Rightarrow 70$, which is the required area estimate.
The rectangles can be seen from the below diagram:

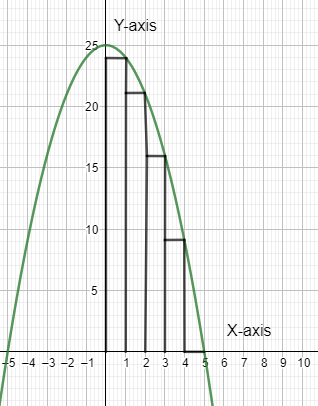
Note:
It is to be noted that the area found is an estimated value and not the real value. The estimated value has some difference between them which is called the error. The same question can be also done by using the left endpoints which are $1,2,3,4,5$. The estimate value in both the cases will differ.