Question

Establish the formula for the capacity of spherical capacitors.

Answer 1

Hint: Capacitance is found by dividing electric charge with voltage by that formula \[C = \dfrac{q}{V}\]

Complete step by step solution:
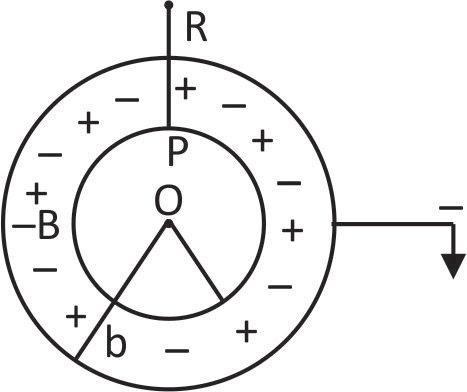
A and B are two \[\infty \]-centric hollow spheres separated by a dielectric medium between them: B is connected to earth. +q charge is given to A and therefore –q charge is included in B in its inner surface. The q charge on the outer surface of B goes to earth.
Radius of A and B be a and b
The potential of A is V = Due to on charge A + induced (–q) of B.
\[V = \dfrac{q}{{4\pi {\varepsilon _0}Ka}} + \dfrac{{ - q}}{{4\pi \varepsilon ab}}\]
\[V = \dfrac{q}{{4\pi {\varepsilon _0}K}}\left[ {\dfrac{1}{a} - \dfrac{1}{b}} \right]\]
\[V = \dfrac{q}{{4\pi {\varepsilon _0}K}}\left[ {\dfrac{{b - a}}{{ab}}} \right]\]

We know,
\[C = \dfrac{q}{v} = C = \dfrac{{\dfrac{q}{q}}}{{4\pi {\varepsilon _0}K}}\left[ {\dfrac{{b - a}}{{ab}}} \right]\]
\[C = 4\pi {\varepsilon _0}K\left[ {\dfrac{{ab}}{{b - a}}} \right]\]

Farad if K = 1 in air or in vacuum
\[C = \dfrac{{4\pi {\varepsilon _0}ab}}{{b - a}}farad\]

Note: The capacitance for spherical conductors can be obtained by evaluating the voltage difference between the conductors for a given charge. It depends on the inner and outer radius of each sphere.