Question

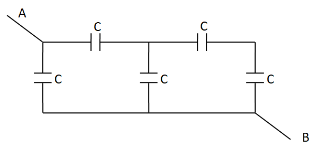
What is the equivalent capacitance of the system of capacitors between A & B?

(A) $ \dfrac{7}{2}C $
(B) $ 1.6C $
(C) $ C $
(D) None

Answer 1

Hint: To solve this question, we need to imagine a battery across the points where the equivalent capacitance is required. Then, identifying the series and parallel combinations, apply the suitable formulae for the equivalent capacitance.

Formula Used: The formulae used in this solution are
 $\Rightarrow \dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} +........... $
 $\Rightarrow {C_p} = {C_1} + {C_2} +........... $
Where $ {C_s} $ is the equivalent series capacitance, and $ {C_p} $ is the equivalent parallel capacitance of the capacitances $ {C_1} $, $ {C_2} $.

Complete step by step answer
In the given circuit diagram, the rightmost two capacitances are connected in series combination. So there equivalent capacitance is
 $\Rightarrow \dfrac{1}{{{C_1}}} = \dfrac{1}{C} + \dfrac{1}{C} $
 $ \Rightarrow \dfrac{1}{{{C_1}}} = \dfrac{2}{C} $
Taking the reciprocal, we get
 $\Rightarrow {C_1} = \dfrac{C}{2} $
So the given circuit diagram can be redrawn as

Now, as we can see in the above figure, the rightmost two capacitances are arranged in parallel combination. So their equivalent capacitance becomes
 $\Rightarrow {C_2} = C + \dfrac{C}{2} $
 $ \Rightarrow {C_2} = \dfrac{{3C}}{2} $
So the above circuit reduces to

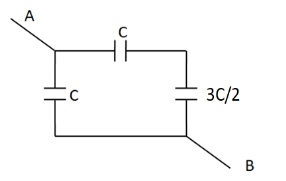
Now, the rightmost two capacitors of capacitances $ C $ and $ \dfrac{{3C}}{2} $ are in series combination. So their equivalent capacitance becomes
 $\Rightarrow \dfrac{1}{{{C_3}}} = \dfrac{1}{C} + \dfrac{2}{{3C}} $
 $ \Rightarrow \dfrac{1}{{{C_3}}} = \dfrac{5}{{3C}} $
Taking the reciprocal, we get
 $\Rightarrow {C_3} = \dfrac{{3C}}{5} $
So the above circuit reduces to

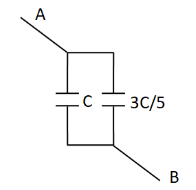
Finally, as we can observe in the above circuit diagram, the two capacitances are arranged in parallel combination. So the equivalent capacitance across A and B becomes
 $\Rightarrow {C_4} = C + \dfrac{{3C}}{5} $
 $ \Rightarrow {C_4} = \dfrac{{8C}}{5} = 1.6C $
Thus the equivalent capacitance between A and B is equal to $ 1.6C $.

Hence, the correct answer is option B.

Note
We should not get confused between the formula of the series and equivalent combinations of resistance and that of the capacitances. The reciprocal relation is valid for the series combination for capacitance and for the parallel combination of the resistances. And the direct addition is valid for the parallel combination for capacitance and for the series combination of the resistances.