Question

What is the equivalent angle of one radian?
(A) ${53.3^ \circ }$
(B) ${54.3^ \circ }$
(C) ${57.3^ \circ }$
(D) ${55.3^ \circ }$

Answer 1

Hint: In order to calculate the angle of any object we have two methods. They are degrees and radians. Radian is one to express an angle. Radian is denoted by the symbol $rad$ which is the S.I. unit for calculating angle of a circle.

Complete step by step solution:
The calculation of radian of a mean angle circle can be explained as the proportion of the distance of the curve of a mean angle circle specific by the angle to that of the distance of the radius of the circle. In order to fully grasp the concept of radian let’s assume a circle of radius of $r$ , mean angle $\theta $ and the specific curve distance $l$. According to the mean angle circle radian is expressed as;

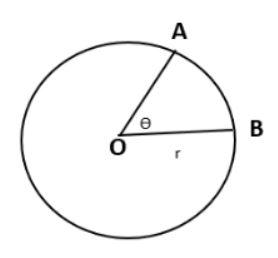
$\theta = \dfrac{l}{r}$
We can constitute $\theta $ as one radian, when $l = r$ ;
$\theta = \dfrac{r}{r}$
$\theta = 1$
For the calculation of one radian in degree;
Let us consider a semicircle where the mean angle is ${180^ \circ }$ . the number of radians that are required to replace the mean angle of the semicircle is more or less equal to $3.14$ $\pi $. Where $\pi $ can be explained as the proportion of the diameter of the circle is divided to the circumference of the circle.
Since $\pi $ is a radian equal to ${180^ \circ }$ we can say that;
$1$ radian $ = \dfrac{{{{180}^ \circ }}}{\pi } = {57.3^ \circ }$

Therefore, one radian is equivalent to ${57.3^ \circ }$

Hence, the option (C), ${57.3^ \circ }$ is the correct answer.

Note: In order to convert to degree to radian the formula is multiply the angle by $\dfrac{\pi }{{{{180}^ \circ }}}$ and in order to convert to radian to degree the formula is multiply the angle by $\dfrac{{{{180}^ \circ }}}{\pi }$ . While solving this problem make sure to draw the diagram of the mean circle and mark the necessary details, it will be helpful in determining the angle.