Question

Equations of tangents to the hyperbola $4{{x}^{2}}-3{{y}^{2}}=24$ which makes an angle of ${{30}^{\circ }}$ with the y – axis are:
(a) $\sqrt{3}x+y=\pm \sqrt{10}$
(b) $\sqrt{3}x+y=\pm 10$
(c) $\sqrt{3}x-y=\pm 5$
(d) $\sqrt{3}x-y=\pm \sqrt{5}$

Answer 1

Hint: First of all write the equation of the given hyperbola $4{{x}^{2}}-3{{y}^{2}}=24$ in the general form which is equal to $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Then we know the equations of tangents to the hyperbola with slope m are equal to $y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}$ . In the above problem, we have given that the tangents are making an angle of ${{30}^{\circ }}$ with the y – axis so the find the angle of tangents made with the x axis because to get the value of the slope we have to find the tangent of the angle made by the line with the positive x axis. Now, after finding the value of slope “m” substitute in the equation of tangents and find the equation of tangents.

Complete step by step answer:
We have given a hyperbola $4{{x}^{2}}-3{{y}^{2}}=24$. We are going to write this equation of a hyperbola in the form of a general equation of a hyperbola.
We know that general form of a hyperbola is equal to:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
So, manipulating the given equation of hyperbola $4{{x}^{2}}-3{{y}^{2}}=24$ in the above form we get,
$4{{x}^{2}}-3{{y}^{2}}=24$
Dividing 24 on both the sides of the above equation we get,
$\begin{align}
  & \dfrac{4}{24}{{x}^{2}}-\dfrac{3}{24}{{y}^{2}}=1 \\
 & \Rightarrow \dfrac{1}{6}{{x}^{2}}-\dfrac{1}{8}{{y}^{2}}=1 \\
 & \Rightarrow \dfrac{{{x}^{2}}}{6}-\dfrac{{{y}^{2}}}{8}=1 \\
\end{align}$
Now, we got the equation of given hyperbola in the form of $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ so the value of a and b in the above equation is equal to:
$\begin{align}
  & {{a}^{2}}=6 \\
 & \Rightarrow a=\pm \sqrt{6} \\
 & {{b}^{2}}=8 \\
 & \Rightarrow b=\pm \sqrt{8} \\
\end{align}$
Now, we have to find the equation of tangents to this given hyperbola.
We know that, equation of tangents for the standard hyperbola of the form $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is equal to:
$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}$..........Eq. (1)
In the above equation, we know the values of a and b but we don’t know the values of m. For m, it is given in the question that the tangents are making an angle of ${{30}^{\circ }}$ with the y axis.
In the below diagram, we are demonstrating if a line makes an angle of ${{30}^{\circ }}$ with the y axis then what is the angle that the same line makes with the positive x axis.

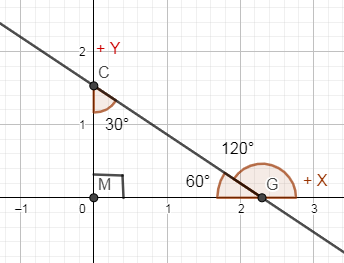
In the above diagram, you can see that the line is making an angle of ${{120}^{\circ }}$ with the positive axis as we have assumed this line as the tangents so basically, the tangents are making an angle of ${{120}^{\circ }}$ with positive x axis.
Now, we have to find the slope “m” of the tangents. We know that, slope of any line is equal to the tangent of the angle made by the line with the positive x axis and we have derived above that the tangents are making an angle of ${{120}^{\circ }}$ with positive x axis. Hence, the slope of these tangents is equal to tangent of ${{120}^{\circ }}$.
Slope (m) of the tangents to the hyperbola is equal to:
$\begin{align}
  & m=\tan {{120}^{\circ }} \\
 & \Rightarrow m=\tan \left( {{90}^{\circ }}+{{30}^{\circ }} \right) \\
\end{align}$
There is a property of tan of the certain angle composition that:
$\tan \left( {{90}^{\circ }}+\theta \right)=-\cot \theta $
Using this property in finding the value of m we get,
$\begin{align}
  & m=-\cot {{30}^{\circ }} \\
 & \Rightarrow m=-\sqrt{3} \\
\end{align}$
Substituting the above value of m and ${{a}^{2}}=6,{{b}^{2}}=8$ in eq. (1) we get,
$\begin{align}
  & y=-\sqrt{3}x\pm \sqrt{6{{\left( -\sqrt{3} \right)}^{2}}-8} \\
 & \Rightarrow y=-\sqrt{3}x\pm \sqrt{6\left( 3 \right)-8} \\
 & \Rightarrow y=-\sqrt{3}x\pm \sqrt{18-8} \\
 & \Rightarrow y=-\sqrt{3}x\pm \sqrt{10} \\
 & \Rightarrow \sqrt{3}x+y=\pm \sqrt{10} \\
\end{align}$
Hence, we got the equations of tangents to the hyperbola as:
$\sqrt{3}x+y=\pm \sqrt{10}$
So, the correct answer is “Option A”.

Note: The mistake that could possible in this problem is that you might have taken the angle that tangents of the hyperbola made with the positive x axis is ${{60}^{\circ }}$ because you think that it is given that tangents are making ${{30}^{\circ }}$ with the positive y axis and as the angle between x and y axis is ${{90}^{\circ }}$ so the angle made by the tangents with positive x axis is the difference of ${{90}^{\circ }}$ and ${{30}^{\circ }}$. This angle is incorrect because the angle that you are getting is in clockwise direction from x axis and the angle that we take from positive x axis is always anticlockwise which you can see from the following figure:

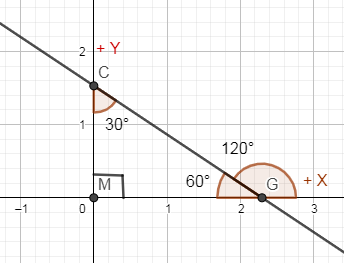
In the above figure, when we go from positive x axis to line CG through angle ${{60}^{\circ }}$ then the angle formed is clockwise whereas if we go from positive x axis to the line CG through angle ${{120}^{\circ }}$ then the direction of traversing is anticlockwise.