Question

What is the equation of the tangent line of $y=\dfrac{1}{x}$ at $x=1$?

Answer 1

Hint: We are given the equation of a rectangular hyperbola here. To find the equation of a tangent line, we need to first calculate the derivative to find the slope and simply use the formula to calculate the tangent line. After that we just plug in the values given in the question and the result would be obtained easily.

Complete step by step solution:
We are given $y=\dfrac{1}{x}$, which is the equation of a rectangular hyperbola. We first need to find the slope of the tangent line. For that we calculate the derivative of the given function.
$\dfrac{dy}{dx}=\dfrac{d\left( \dfrac{1}{x} \right)}{dx}$
We can write $\dfrac{1}{x}$ as $x^{-1}$. And after that we use the formula below:
$\dfrac{d\left(x^{-1}\right)}{dx}=-1\times x^{-2}$
Hence, the derivative is calculated.
Now, we plug the value of the point given to find the slope at that point. Let the slope be ‘m’, then:
$m=\dfrac{dy}{dx}=-1\times x^{-2}$
At $x=1$, the slope will be:
$m=-\left(1\right)^2=-1$
Now, we have the x-coordinate given in the question, but we need to find the y-coordinate as well. For that we use the fact that $x=1$ will satisfy the equation of the hyperbola given, so we put $x=1$ in the equation of the hyperbola and we get:
$y=\dfrac{1}{x}=\dfrac{1}{1}=1$
Now, we put these values obtained in the point slope form of the line to get the tangent line equation:
$\left(y-y_1\right)=m\times\left(x-x_1\right)$
Here, $m=-1$, $x_1=1$ and $y_1=1$.
Putting these values we get:
$\left(y-1\right)=-1\times\left(x-1\right)$
$\implies y-1=-x+1$
$\implies y+x=2$
Hence, the equation of tangent line is obtained.
The graph of the curve along with its tangent line is shown below:

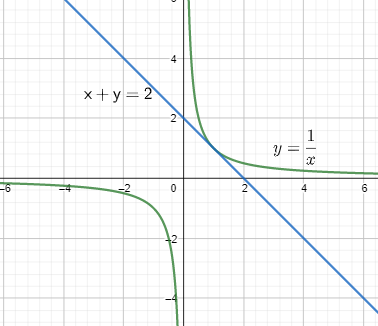
Note: While taking variables on the other side of the equation, do not forget to change the sign. In the point slope form, put the values carefully, because it might lead to a different tangent line which would result in a wrong solution.