
What is the equation of the parabola with a focus at \[\left( -2,6 \right)\] and a vertex at \[\left( -2,9 \right)\] ?
Answer
524.4k+ views
Hint: These types of problems are very simple and easy to solve. We can solve this problem efficiently once we understand the key concepts behind these types of questions. The problem is of coordinate geometry of sub-topic parabola, and for solving it we need to first know what the different general forms of parabolas are that are possible in coordinate geometry. There are four general types of parabola and for each of them, the corresponding vertex and foci are as follows,
Complete step-by-step solution:
Now, starting off with the solution of our given problem by writing that, here we first of all need to find the value of the length of the latus rectum which is denoted by \[4a\] . The distance between the vertex and the foci of a parabola is denoted by ‘a’. We now find the value of ‘a’ by finding the distance between the vertex and the foci,
\[\begin{align}
& a=\sqrt{{{\left( -2-\left( -2 \right) \right)}^{2}}+{{\left( 6-9 \right)}^{2}}} \\
& \Rightarrow a=\sqrt{{{3}^{2}}} \\
& \Rightarrow a=3 \\
\end{align}\]
Now the value of \[4a\] will be equal to,
\[4a=12\]
Now, in this problem we see that the vertex is above the foci and they are on the same vertical line. From this we can easily conclude that the given parabola will be of the form \[{{x}^{2}}=-4ay\] . Here applying the change for the origin we get the equation of the parabola as,
\[{{\left( x-h \right)}^{2}}=-4a\left( y-k \right)\]
Here \[\left( h,k \right)\] are the coordinates of the vertex.
Therefore the equation of the parabola is,
\[\begin{align}
& {{\left( x+2 \right)}^{2}}=-12\left( y-9 \right) \\
& \Rightarrow {{x}^{2}}+4+4x=-12y+108 \\
& \Rightarrow {{x}^{2}}+4x+12y-104=0 \\
\end{align}\]
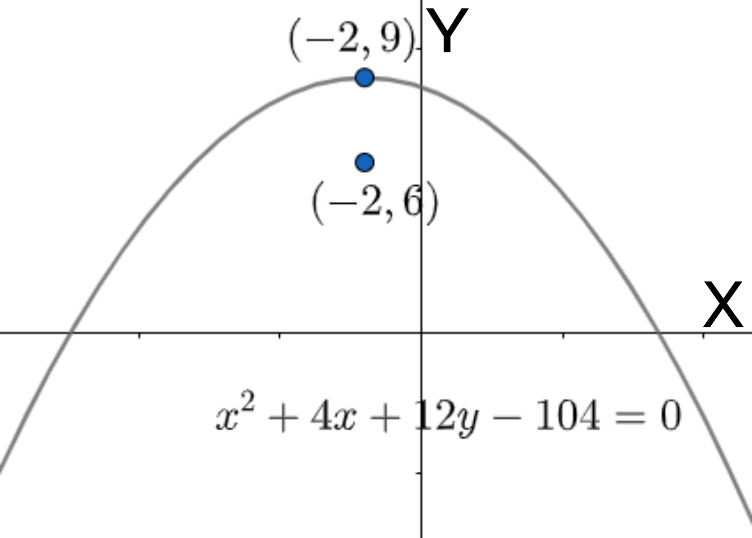
Note: For solving these types of problems, we need to have a clear cut idea of coordinate geometry and parabola. We can also solve this problem in another method by using a graph paper. Here, we plot the vertex and the foci and then draw the parabola accordingly. But it is a lengthier process and is more time consuming. We need to be very careful while we are shifting the origin of the parabola, as it is prone to errors.
| Equation | Vertex | Foci |
| \[{{y}^{2}}=4ax\] | \[\left( 0,0 \right)\] | \[\left( a,0 \right)\] |
| \[{{y}^{2}}=-4ax\] | \[\left( 0,0 \right)\] | \[\left( -a,0 \right)\] |
| \[{{x}^{2}}=4by\] | \[\left( 0,0 \right)\] | \[\left( 0,b \right)\] |
| \[{{x}^{2}}=-4by\] | \[\left( 0,0 \right)\] | \[\left( 0,-b \right)\] |
Complete step-by-step solution:
Now, starting off with the solution of our given problem by writing that, here we first of all need to find the value of the length of the latus rectum which is denoted by \[4a\] . The distance between the vertex and the foci of a parabola is denoted by ‘a’. We now find the value of ‘a’ by finding the distance between the vertex and the foci,
\[\begin{align}
& a=\sqrt{{{\left( -2-\left( -2 \right) \right)}^{2}}+{{\left( 6-9 \right)}^{2}}} \\
& \Rightarrow a=\sqrt{{{3}^{2}}} \\
& \Rightarrow a=3 \\
\end{align}\]
Now the value of \[4a\] will be equal to,
\[4a=12\]
Now, in this problem we see that the vertex is above the foci and they are on the same vertical line. From this we can easily conclude that the given parabola will be of the form \[{{x}^{2}}=-4ay\] . Here applying the change for the origin we get the equation of the parabola as,
\[{{\left( x-h \right)}^{2}}=-4a\left( y-k \right)\]
Here \[\left( h,k \right)\] are the coordinates of the vertex.
Therefore the equation of the parabola is,
\[\begin{align}
& {{\left( x+2 \right)}^{2}}=-12\left( y-9 \right) \\
& \Rightarrow {{x}^{2}}+4+4x=-12y+108 \\
& \Rightarrow {{x}^{2}}+4x+12y-104=0 \\
\end{align}\]

Note: For solving these types of problems, we need to have a clear cut idea of coordinate geometry and parabola. We can also solve this problem in another method by using a graph paper. Here, we plot the vertex and the foci and then draw the parabola accordingly. But it is a lengthier process and is more time consuming. We need to be very careful while we are shifting the origin of the parabola, as it is prone to errors.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




