Question

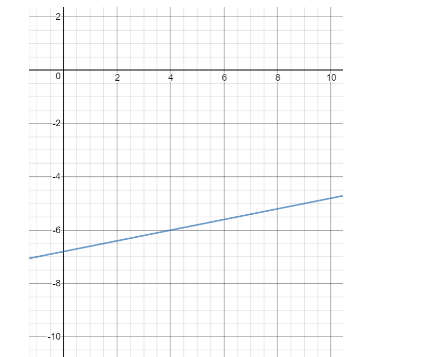
What is the equation of the line shown in the graph in slope-intercept form?

Answer 1

Hint: In this question, we are given the graph of a straight line and we have to find the equation of this line. All the points lying on the graph of a line satisfy its equation, so we can find any number of points lying on the graph. We can find the equation of a line if its slope and one passing point is known to us, so we will find the coordinates of two points lying on this line. From those two points, we can find the slope of the line and we can take one of the points as the passing point.

Complete step-by-step answer:
From the graph, we see that $ (4, - 6) $ and $ (9, - 5) $ lie on this line.
We know that the slope of a line is given as –
 $
  slope = \dfrac{{change\,in\,y}}{{change\,in\,x}} \\
  slope = \dfrac{{ - 5 - ( - 6)}}{{9 - 4}} \\
   \Rightarrow slope = \dfrac{1}{5} \\
  $
Now, the equation of a line is given as –
 $ y - {y_1} = m(x - {x_1}) $ where $ m $ is the slope of the line and $ ({x_1},{y_1}) $ is a point through which the line passes.
Here $ (4, - 6) $ is one of the passing points, so the equation of the line is –
 $
  y - ( - 6) = \dfrac{1}{5}(x - 4) \\
   \Rightarrow y + 6 = \dfrac{1}{5}x - \dfrac{4}{5} \\
   \Rightarrow y = \dfrac{1}{5}x - \dfrac{{34}}{5} \\
  $
Hence the equation of the line in slope-intercept form is $ y = \dfrac{1}{5}x - \dfrac{{34}}{5} $
So, the correct answer is “ $ y = \dfrac{1}{5}x - \dfrac{{34}}{5} $ ”.

Note: The equation of straight line contains the unknown variables in degree 1 so it is known as a linear equation. A linear equation is expressed in terms of two unknown variable quantities namely x and y. A linear equation can be expressed in several forms, and one such way is slope-intercept form. In this form, we express y in terms of the slope, x and the y-intercept.