Question

Equation of tangent to the circle, at the point $\left( {1, - 1} \right)$ whose centre is the point of intersection of the straight lines $x - y = 1\,\,\& \,\,2x + y = 3$ is:

Answer 1

Hint: In order to solve the question find the point of intersection of the two given lines that will be the centre of the circle. Using that find the slope of the radius at the point $\left( {1, - 1} \right)$. Then, find the slope of the tangent at the point $\left( {1, - 1} \right)$ and write the equation.

Complete step-by-step solution:
As stated in the question, the center of the circle is the point of intersection of the straight lines $x - y = 1\,\,\& \,\,2x + y = 3$
Now we will find the intersection of these lines
$\
\Rightarrow x - y = 1\,\,\,\,\,\,\,\, \to \left( 1 \right) \\
\Rightarrow 2x + y = 3\,\,\,\,\,\, \to \left( 2 \right) \\
\ $
From (1) and (2) we get
$\
\Rightarrow 3x = 4\,\,\, \\
\Rightarrow x = \dfrac{4}{3} \\
\ $
Using it in (1) we get
$y = \dfrac{1}{3}$
Therefore the center of the circle is $\left( {\dfrac{4}{3},\dfrac{1}{3}} \right)$, as shown in the below figure.

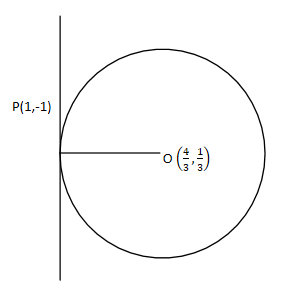
Now if we find the slope of the radius at the point $\left( {1. - 1} \right)$ we can find the slope of the tangent from which we can get the equation of the tangent.
Slope of two points $\left( {{x_1},{y_1}} \right)\,\,\,\& \,\,\left( {{x_2},{y_2}} \right)$
$ = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
By using the above formula we get the slope of line of radius $\left( {\dfrac{4}{3},\dfrac{1}{3}} \right)\,\,\,\& \,\,\left( {1. - 1} \right)$ as
$\dfrac{{ - 1 - \dfrac{1}{3}}}{{1 - \dfrac{4}{3}}} = 4$
As we all know the line from the center to a point on the circle is perpendicular to tangent at that point.
Also the product of slope of two lines is $ - 1$
i.e. The condition for slope of two perpendicular lines
Let us assume that slope of tangent is $m$ .Then
$\
\Rightarrow 4 \times m = - 1 \\
\Rightarrow m = - \dfrac{1}{4} \\
\ $
Therefore slope of tangent is $ - \dfrac{1}{4}$
Now we need to write the equation of tangent in slope from equation of tangent in slope form
$\dfrac{{y - k}}{{x - h}} = m$
Where $\left( {h,k} \right)$ is the point at which tangent is to be drawn.
Hence equation of tangent becomes,
$\
\Rightarrow \dfrac{{y + 1}}{{x - 1}} = - \dfrac{1}{4} \\
\Rightarrow 4y + 4 = 1 - x \\
\Rightarrow 4y + x + 3 = 0 \\
\ $

Therefore the equation of the tangent is $ 4y + x + 3 = 0$.

Note: In order to solve such questions remembering the formulas and equations is very important such as formula for slope of line in point form, equation of tangent in point form, etc. without these we won’t be able to solve the question. Also, calculating the values carefully is very important as these are chances of mistakes.