Question

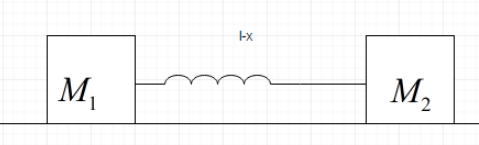
Equation of length of the spring as a function of time is given by x?

A. \[1-{{A}_{1}}\cos wt\]
B. \[1-({{A}_{1}}+{{A}_{2}})\cos wt\]
C. \[({{A}_{1}}+{{A}_{2}})\cos wt\]
D. \[1-{{A}_{2}}\cos wt\]

Answer 1

Hint:We are given a stretched spring between the two masses. The spring constant of the spring is k.We have to take some point as origin and then from that point we can measure the equilibrium length which is unstretched and also the extension of the spring.

Complete step by step answer:
We know spring has a spring of force constant, $k$ and it has the tendency to return to its equilibrium position that is the unstretched position when it is either compressed or stretched. The energy possessed by the spring when it is either stretched or compressed is called its potential energy.We assume that the equilibrium position of 1st particle be at origin i.e. x = 0. $x$ coordinate of particles can be written as:
\[{{x}_{1}}={{A}_{1}}\cos wt\] and \[{{x}_{2}}=1-{{A}_{1}}\cos wt\]
Thus, the length of spring at time t can be written as:
\[\therefore{{x}_{2}}-{{x}_{1}}=1-({{A}_{1}}+{{A}_{2}})\cos wt\]

So, the correct option is B.

Note: The equilibrium state of the spring corresponds to the situation in which the spring is stretched or we can say that the spring is unextended. But if the spring is perturbed from its equilibrium state then a restoring force comes into play which can be written in the form: \[f(x)=-kx\], where k is the spring constant and x is the extension in the length. Using second law, \[m\dfrac{{{\partial }^{2}}x}{\partial {{t}^{2}}}=-kx\]
This differential equation is we say as the simple harmonic oscillator equation, and its solution is known to us. The solution is \[x=A\cos wt\]. Thus, from here we came to use cos to write the solution that we have done in this problem.