Question

When is an equation called an ‘identity’. Prove the trigonometric identity $1 + {\cot ^2}A = \cos e{c^2}A$?

Answer 1

Hint: The given problem deals with the basic concepts and formulae of trigonometric functions. The given question requires us to prove a trigonometric identity.These types of trigonometric identities or formulae can be proved by considering a right angled triangle and then calculating the trigonometric ratios. We will first calculate the trigonometric functions cotangent and cosecant for an angle and then use Pythagoras theorem to make the left side of the equation equal to the right side of the equation.

Complete step by step answer:

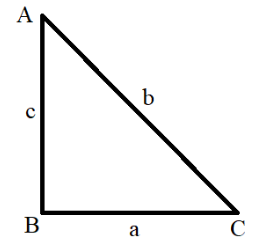
So, we have to prove the trigonometric identity $1 + {\cot ^2}A = \cos e{c^2}A$ .Consider a right angled triangle ABC, in which $\angle B = {90^ \circ }$. Then, AC $ = $ Hypotenuse, AB $ = $ Base for $\angle A$, BC $ = $ Perpendicular for$\angle A$. Now, we will find the value of trigonometric ratios cotangent and cosecant for the angle A in the triangle ABC. So, we know that $\cot \theta = \dfrac{{{\text{Base}}}}{{{\text{Perpendicular}}}}$ and $\cos ec\theta = \dfrac{{{\text{Hypotenuse}}}}{{{\text{Perpendicular}}}}$. So, we get, $\cot A = \dfrac{{AB}}{{{\text{BC}}}} = \dfrac{c}{a}$ and $\cos ecA = \dfrac{{{\text{AC}}}}{{{\text{BC}}}} = \dfrac{b}{a}$

Now, we simplify both sides of the equation $1 + {\cot ^2}A = \cos e{c^2}A$ to prove the equality by making the left side of the equation equal to the right side. So, we get,
$L.H.S. = 1 + {\cot ^2}A$
Substituting the value of cotangent of angle A, we get,
$L.H.S. = 1 + {\left( {\dfrac{c}{a}} \right)^2}$
Now, taking LCM and simplifying the expression, we get,
$L.H.S.= \dfrac{{{a^2} + {c^2}}}{{{a^2}}}$
Now, we know the Pythagoras Theorem. So, we have, ${\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Altitude} \right)^2}$.
Hence, ${b^2} = {a^2} + {c^2}$.

So, we substitute the value of ${a^2} + {c^2}$ in the expression.
$\dfrac{{{b^2}}}{{{a^2}}}$
Now, we simplify the right side of the trigonometric identity $1 + {\cot ^2}A = \cos e{c^2}A$.
$R.H.S. = \cos e{c^2}A$
Substituting the value of cosecant of angle A in the expression, we get,
$R.H.S. = {\left( {\dfrac{b}{a}} \right)^2}$
$\Rightarrow R.H.S. = \dfrac{{{b^2}}}{{{a^2}}}$
Hence, we get the left side of the identity equals the right side.
So, $1 + {\cot ^2}A = \cos e{c^2}A$.
Hence, Proved.

Note: The above problem tells us about the difference between an equation and an identity. We must know the basic definitions of both the terms to answer the problem. We must know the formulae of trigonometric ratios in order to tackle such problems. One must also know about the applications of the Pythagoras Theorem.