Question

How many envelopes can be made of sheet of handmade paper \[1\text{ }m\text{ }25\text{ }cm\] by \[85\text{ }cm\]. If each envelope requires a piece of paper of size \[17\text{ }cm\] by \[5\text{ }cm\]? Rohan made those envelopes and sold them at \[Rs.\text{ }12.50\] each. What amount does he collect?

Answer 1

Hint: To find the number of envelopes and pricing we divide the area of the handmade paper to the area of the envelope and to find the pricing we multiply the price of a single envelope with the divided result to find the total price of all the envelopes formed. The formula used to find the total numbers of envelopes are:
Total number of envelopes \[=\dfrac{Area{}_{Paper}}{Are{{a}_{Envelope}}}\]

Complete step by step answer:
The total price of all the envelopes \[=\dfrac{Area{}_{Paper}}{Are{{a}_{Envelope}}}\times \text{Pric}{{\text{e}}_{\text{single envelope}}}\]
The handmade paper is given in a diagram as shown below:

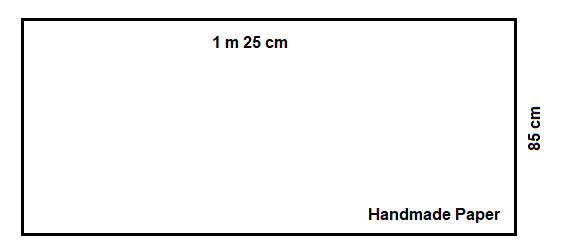
And similarly, the envelopes made from it, are also shown below as:

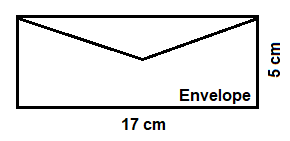
Hence, the comparison is,

Now putting the values in the formula to find the total number of envelope
Total number of envelopes \[=\dfrac{Area{}_{Paper}}{Are{{a}_{Envelope}}}\]
Hence, the area of the paper is \[Area{}_{Paper}=1.25\text{ }m\times 85\text{ }cm\]
Converting the dimension of $1m\, 25 cm $ into $cm$ that is \[125\text{ }cm\]
\[=125\text{ c}m\times 85\text{ }cm\]
\[=10625\text{ }c{{m}^{2}}\]
And the area of a single envelope is \[Area{}_{Envelope}=17\text{ c}m\times 5\text{ }cm\]
\[=17\text{ c}m\times 5\text{ }cm\]
\[=85\text{ }c{{m}^{2}}\]
Therefore, Total number of envelopes \[=\dfrac{Area{}_{Paper}}{Are{{a}_{Envelope}}}\]
\[=\dfrac{10625\text{ }c{{m}^{2}}}{85\text{ }c{{m}^{2}}}\]
\[=125\]
Now checking the total price of all the envelopes we multiply the price of a single envelope by total number of envelope
\[=\dfrac{Area{}_{Paper}}{Are{{a}_{Envelope}}}\times\text{Pric}{{\text{e}}_{\text{single envelope}}}\]
\[=125\times \text{Rs}\text{.12}\text{.50}\]
\[=Rs.\text{ }1562.5\]

Hence, the amount of money collected by all the envelopes sold from a single handmade paper is \[Rs.\text{ }1562.5\].

Note:
Students may go wrong while taking the dimensions of the handmade paper as all the dimensions, be it paper or envelope are given in centimeter except the length of the handmade paper which is given in meter and centimeter hence, it is necessary to either convert it into centimeter or convert other dimensions into meters and then proceed with the question.