Question

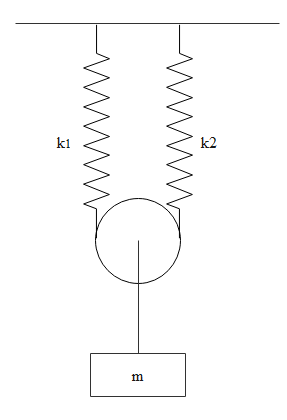
What is the elongation in the two springs.

Answer 1

Hint: This problem can be solved just like we solve the pulley string problem. The weight of the block will transfer to the string attached to it and then it will transfer to the two springs attached to it. Tension produced in each spring will be equal to its spring force.
Formula used:
$T = kx$

Complete answer:
When the block is attached to the pulley, due to its weight tension is created in the string which is attached to the pulley.
Now this pulley is attached to the two springs. Here our assumptions are pulley is massless and string is massless and springs are also massless. There is no friction between the pulley and the string or springs.
If there is friction and pulleys have a mass then torque will be acted on pulleys due to friction and then pulley will rotate.
The weight of the block is
$W = mg$
This weight will be the tension in the string which is attached to the pulley.
Now this tension will be divided among the springs.
Since there will be a string which will be connecting two springs and holds the pulley in position, the two springs can be assumed to be connected through that string.
So tension in both springs will be the same in both the springs.

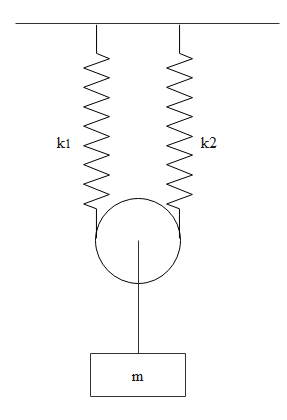
Let us assume the tension in the springs is ‘T’
$\eqalign{
  & T + T = mg \cr
  & \Rightarrow 2T = mg \cr
  & \Rightarrow T = \dfrac{{mg}}{2} \cr} $
So the spring force in the spring is nothing but the tension in the spring. So the formula for the tension will be $T = kx$
Where
T is the tension in the spring
K is the spring constant of the spring
‘x’ is the elongation produced in the spring due to the tension.
So
$T = kx$
$\eqalign{
  & \Rightarrow T = {k_1}{x_1} \cr
  & \Rightarrow T = {k_2}{x_2} \cr
  & \Rightarrow {k_1}{x_1} = \dfrac{{mg}}{2} \cr
  & \Rightarrow {k_2}{x_2} = \dfrac{{mg}}{2} \cr
  & \Rightarrow {x_1} = \dfrac{{mg}}{{2{k_1}}} \cr
  & \Rightarrow {x_2} = \dfrac{{mg}}{{2{k_2}}} \cr
  & \Rightarrow {x_1} + {x_2} = \dfrac{{mg}}{{2{k_1}}} + \dfrac{{mg}}{{2{k_2}}} \cr} $
Hence we have got the elongation produced in first spring as ${x_1} = \dfrac{{mg}}{{2{k_1}}}$ and in the second spring as ${x_2} = \dfrac{{mg}}{{2{k_2}}}$ and total elongation will be ${x_1} + {x_2} = \dfrac{{mg}}{{2{k_1}}} + \dfrac{{mg}}{{2{k_2}}}$

Note:
The same procedure can be followed to find out the effective spring constant of a system so that we can find out the time period of oscillations if the small displacement is given to the block.