Question

Electric field outside a long wire carrying charge q is proportional to:
$
  {\text{A}}{\text{. }}\dfrac{1}{r} \\
  {\text{B}}{\text{. }}\dfrac{1}{{{r^2}}} \\
  {\text{C}}{\text{. }}\dfrac{1}{{{r^{\dfrac{1}{{3/5}}}}}} \\
  {\text{D}}{\text{. }}\dfrac{1}{{{r^{\dfrac{1}{{3/2}}}}}} \\
 $

Answer 1

Hint: We need to use the Gauss law to obtain the expression for the electric field outside a long wire carrying a charge q. From the obtained expression, we can check the dependence of the electric field on distance r from the wire which will give us the required answer.
Formula used:
Gauss law is given as
$\oint {\overrightarrow E .\overrightarrow {dS} = \dfrac{{{q_{net}}}}{{{ \in _0}}}} $

Complete answer:
We are given a long cylindrical wire as shown in the following diagram.

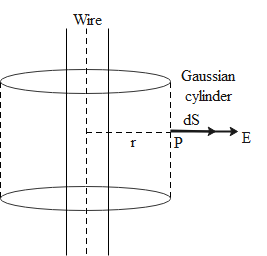
It carries a total charge q and the amount of charge per unit length of the wire can be written as
$
  \lambda = \dfrac{q}{l} \\
  q = \lambda l \\
 $
Here l signifies the length of the wire. Now consider a point P outside this wire at distance r where we want to calculate the electric field due to the wire. Since we are going to use the Gauss law for this, we also need to construct a Gaussian surface around it.
For a cylindrical wire the Gaussian surface will look like a cylinder whose radius is r. Now we can apply the Gauss law to this cylinder in the following way.
$\oint {\overrightarrow E .\overrightarrow {dS} = \dfrac{{{q_{net}}}}{{{ \in _0}}}} $
Here dS is the small area element on the Gaussian cylinder. We can solve this in the following way.
$
  E\int {dS} = \dfrac{q}{{{ \in _0}}} = \dfrac{{\lambda l}}{{{ \in _0}}} \\
   \Rightarrow E \times 2\pi rl = \dfrac{{\lambda l}}{{{ \in _0}}} \\
  \therefore E = \dfrac{\lambda }{{2\pi { \in _0}r}} \\
 $
This is the final expression for the electric field due to the wire at a distance r outside it. We see that $E \propto \dfrac{1}{r}$.

Therefore, the correct dependence of E on distance is option A.

Note:
It should be noted that the direction of the electric field and the area element is the same. Due to this, $\overrightarrow E .\overrightarrow {dS} = EdS\cos 0^\circ = EdS$. Also, the electric field due to the wire is constant since the charge on the wire is also constant, so we have taken E out of the integral in the above calculation.