Question

When an elastic material with Young’s modulus Y is subjected to stretching stress S, elastic energy stored per unit volume of the material is
$\begin{array}{rl}& a){\displaystyle \frac{YS}{2}}\\ & b){\displaystyle \frac{S^{2}Y}{2}}\\ & c){\displaystyle \frac{S^2}{2Y}}\\ & d){\displaystyle \frac{S}{2Y}}\end{array}$

Answer 1

Hint: When an elastic material is subjected to stretching stress, the work done in stretching it is stored in the form of potential energy in the wire. Let us say we extend the wire of length L, area of cross section A and Young’s modulus Y by $\mathrm{\Delta }L$(change in length), Then the required force is $F={\displaystyle \frac{Y.A.\mathrm{\Delta }L}{L}}...(1)$. From this expression we can see that the force acting is a variable force. Hence we need to integrate the required work done by the above action of force.

Complete answer:
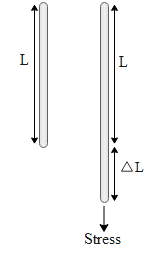
In the above diagram we can see that the wire of length L gets extended to a final length of $L+\mathrm{\Delta }L$. From the beginning let us say we start to extend the wire and we extend it to a length x from the initial length L. Furthermore we want to extend it by a small length dx. The work done in doing so is given by,
$E=F.dx,\text{where F is the is applied force}$. Substituting equation 1 for F and integrating the work done for extending the wire we get,
$\begin{array}{rl}& E=\underset{0}{\overset{\mathrm{\Delta }L}{\int }}\left({\displaystyle \frac{Y.A.x}{L}}\right)dx\\ & \Rightarrow E={\displaystyle \frac{YA}{L}}\underset{0}{\overset{\mathrm{\Delta }L}{\int }}xdx\\ & \Rightarrow E={\displaystyle \frac{YA}{L}}{\left[{\displaystyle \frac{x^2}{2}}\right]}_0^{\mathrm{\Delta }L}\\ & \Rightarrow E={\displaystyle \frac{YA}{2L}}[\mathrm{\Delta }{L}^2-0]\\ & \Rightarrow E={\displaystyle \frac{YA\mathrm{\Delta }{L}^2}{2L}}\end{array}$

Multiplying and dividing by L the above equation we get,
$E={\displaystyle \frac{YA{\left(\mathrm{\Delta }L\right)}^{2}L}{2L^2}}$
The term ${\displaystyle \frac{\mathrm{\Delta }L}{L}}$ is the strain in the material and the term AL represents the volume (V)of the material.
Hence the above equation becomes,
$\begin{array}{rl}& E={\displaystyle \frac{Y\left(AL\right)}{2}}{\left({\displaystyle \frac{\mathrm{\Delta }L}{L}}\right)}^2\\ & E={\displaystyle \frac{YV{\left(strain\right)}^2}{2}}....(2)\end{array}$
The Young’s modulus for a wire is given by stress (S) by strain i.e. $Y={\displaystyle \frac{S}{strain}}$hence substituting for strain in equation 2 we get,
$\begin{array}{rl}& E={\displaystyle \frac{YV}{2}}{\left({\displaystyle \frac{S}{Y}}\right)}^2\\ & E={\displaystyle \frac{V{S}^2}{2Y}}\text{ hence energy per unit volume is,}\\ & {\displaystyle \frac{E}{V}}={\displaystyle \frac{S^2}{2Y}}\end{array}$

So, the correct answer is “Option C”.

Note:
The above condition is analogous to potential energy of a spring. As we extend the spring the force required is directly proportional to the length of extension. If we still want to extend it further more and more force is required to extend any further.