Question

Eccentricity of ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ such that the line joining the foci subtends a right angle only at two points on ellipse is
a) $\dfrac{1}{2}$
b)$\dfrac{1}{\sqrt{2}}$
c)$\dfrac{1}{\sqrt{3}}$
d) $\dfrac{1}{\sqrt{5}}$

Answer 1

Hint: By looking at the equation, we must find the slope of BS and BS’ by using the formula given below. As it is given that the angle made here is $90{}^\circ $ use the condition of perpendicularity. If 2 lines of slope m, n are perpendicular then \[\left( m\cdot n \right)=-1\] . By the above equation find the relation between a, b where a is semi major axis and b is semi minor axis. Use the relation between a, b, e already present. So, substitute b in terms of a, e to cancel the a and find the value of e. Use the following formulae of ellipse.

Slope of BS $=\dfrac{-b}{ae}$ ; (ii) slope of BS’ $=\dfrac{b}{ae}$ ; (iii) \[{{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)\]

Complete step-by-step answer:
Ellipse: In mathematics, ellipse is a plane curve surrounded by 2 points called foci, such that for all points on the curve the sum of distances from the 2 points is a constant. By this, we can see it generates a circle. So, we say it is a special type of ellipse with both foci coinciding with each other.

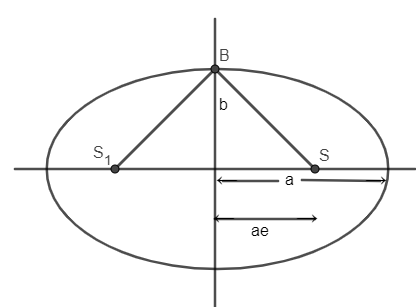
Given equation of an ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$

Let the slope of BS’ line be assumed as variable is n.

Let the slope of the BS line be assumed as a variable m.

By basic knowledge of ellipse, we can say formulae.

Slope of BS \[=\dfrac{-b}{ae}=m\] , slope of BS’ \[=\dfrac{b}{ae}=n\]

By condition of perpendicular if slopes x, y perpendicular \[\Rightarrow \left( x\cdot y \right)=-1\] ; here m, n are perpendicular.

By substituting we set the equation as : \[\left( m\cdot n \right)=-1\]

\[-{{\left( \dfrac{b}{ae} \right)}^{2}}=-1\text{ }\Rightarrow {{b}^{2}}={{a}^{2}}{{e}^{2}}\]

By basic knowledge of ellipse, we have \[{{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)\]

By this, we turn equation into \[{{a}^{2}}\left( 1-{{e}^{2}} \right)={{e}^{2}}{{a}^{2}}\]

By cancelling the ${{a}^{2}}$ term on both sides on equation, we get:

\[1-{{e}^{2}}={{e}^{2}}\]

By adding ${{e}^{2}}$ on both sides and dividing with 2 on both sides, we get

${{e}^{2}}=\dfrac{1}{2}$

By applying square root on both sides of equation, we get:

$e=\pm \dfrac{1}{\sqrt{2}}$

By options we say $e=\dfrac{1}{\sqrt{2}}$

Therefore, option (B) is the correct answer for a given question.


Note: (1) Here, eccentricity can be negative but from options we take one root and exclude the other. (2) We took BS, BS’ as the given perpendicular for easy calculation. You take the general point instead of B for general proof but it will be a long way.