Question

What is the eccentricity of a rectangular hyperbola?
(a). \[\sqrt 2 \]
(b). \[\sqrt 3 \]
(c). \[\sqrt 5 \]
(d). \[\sqrt 6 \]

Answer 1

Hint: When the transverse axis of a hyperbola is equal to its conjugate axis then the hyperbola is called a rectangular hyperbola. The eccentricity e of the hyperbola is given by \[e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}\]. Use this formula to calculate the eccentricity.

Complete step-by-step solution -
A hyperbola is a curve generated by a point moving such that the difference of the distances from two fixed points is constant. Its equation is given by:
\[\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\]

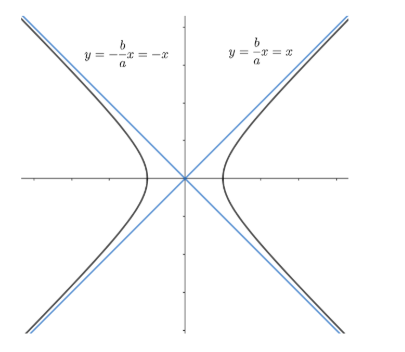
If the transverse axis of the hyperbola, represented by a, is equal to its conjugate axis, represented by b, then the hyperbola is called a rectangular hyperbola. The asymptotes are x = y and x = - y. Hence, we have as follows:
\[a = b............(1)\]
Eccentricity is a measure of how nearly circular the curve is. It is defined as the ratio of the distance from the center to the focus and the distance from the center to the vertex.
The eccentricity of a hyperbola is always greater than 1. The eccentricity of a hyperbola with the equation \[\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\] is given as follows:
\[e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}\]
Substituting equation (1) in the above equation, we have:
\[e = \dfrac{{\sqrt {{a^2} + {a^2}} }}{a}\]
Simplifying, we have:
\[e = \dfrac{{\sqrt {2{a^2}} }}{a}\]
\[e = \dfrac{{\sqrt 2 a}}{a}\]
Canceling the common terms in the numerator and denominator, we have:
\[e = \sqrt 2 \]
The eccentricity of a rectangular hyperbola is \[\sqrt 2 \].
Hence, the correct answer is option (a).

Note: You need to know the concepts of the eccentricity of the hyperbola to be able to solve this question. The formula for the eccentricity of a hyperbola is \[e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}\]. You can also find the focus first and then find the ratio to get the eccentricity.