Question

What is the eccentric angle in the first quadrant of a point on the ellipse $\dfrac{{{x^2}}}{{10}} + \dfrac{{{y^2}}}{8} = 1$ at a distance 3 units from the centre of the ellipse?
(A). $\dfrac{\pi }{6}$
(B). $\dfrac{\pi }{4}$
(C). $\dfrac{\pi }{3}$
(D). $\dfrac{\pi }{2}$

Answer 1

Hint- In such types of questions, just follow the simple approach first take the parametric equation of ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ centred at origin and find the distance of $x = a\cos \theta ,y = b\sin \theta $ point in the first quadrant from the origin and then equate that to the given distance to get the required value of $\theta $ i.e. the eccentric angle.

Complete step-by-step solution -
Let us suppose the point \[P\] is on the ellipse given.

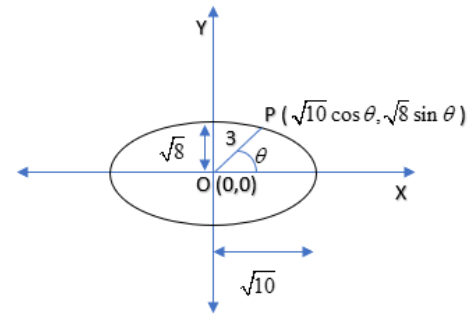
Now we have ${a^2} = 10,{b^2} = 8$ so we have $a = \sqrt {10} ,b = \sqrt 8 $
We have the parametric equation of the ellipse as $x = a\cos \theta ,y = b\sin \theta $ and here $x = \sqrt {10} \cos \theta ,y = \sqrt 8 \sin \theta $
Now, we know that the distance formula to calculate distance between two points say A $(x_1, y_1)$ and B $(x_2, y_2)$ which is $d = \sqrt {{{(x_2 - x_1)}^2} + {{(y_2 - y_1)}^2}} $
Here the two points are $P(\sqrt {10} \cos \theta ,\sqrt 8 \sin \theta )$ and O (0, 0)
So, $d = \sqrt {{{\left( {0 - \sqrt {10} \cos \theta } \right)}^2} + {{\left( {0 - \sqrt 8 \sin \theta } \right)}^2}} $
$ \Rightarrow d = \sqrt {{{\left( { - \sqrt {10} \cos \theta } \right)}^2} + {{\left( { - \sqrt 8 \sin \theta } \right)}^2}} $
\[ \Rightarrow d = \sqrt {10{{\cos }^2}\theta + 8{{\sin }^2}\theta } \]
Now, d = 3 as given in the question so we get,
\[ \Rightarrow 3 = \sqrt {10{{\cos }^2}\theta + 8{{\sin }^2}\theta } \]
Squaring both sides, we get,
\[ \Rightarrow {3^2} = 10{\cos ^2}\theta + 8{\sin ^2}\theta \]
\[ \Rightarrow 9 = 10{\cos ^2}\theta + 8{\sin ^2}\theta \]
Now we know that ${\cos ^2}\theta = 1 - {\sin ^2}\theta $
\[ \Rightarrow 9 = 10(1 - {\sin ^2}\theta ) + 8{\sin ^2}\theta \]
\[ \Rightarrow 9 = 10 - 10{\sin ^2}\theta + 8{\sin ^2}\theta \]
\[ \Rightarrow 10{\sin ^2}\theta - 8{\sin ^2}\theta = 10 - 9\]
\[ \Rightarrow 2{\sin ^2}\theta = 1\]
\[ \Rightarrow {\sin ^2}\theta = \dfrac{1}{2}\]
\[ \Rightarrow \sin \theta = \dfrac{1}{{\sqrt 2 }}\]
We know that $\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$ in the first quadrant.
So, we have $\theta = \dfrac{\pi }{4}$
Hence, the eccentric angle in the first quadrant of a point on the ellipse $\dfrac{{{x^2}}}{{10}} + \dfrac{{{y^2}}}{8} = 1$ at a distance 3 units from the centre of the ellipse is $\theta = \dfrac{\pi }{4}$
$\therefore $ Option B. $\dfrac{\pi }{4}$ is the correct answer.

Note- In such types of questions, just keep in mind the distance formula to calculate the distance between two points i.e. for two points say two points say A $(x_1, y_1)$ and B $(x2, y2)$ distance is $d = \sqrt {{{(x_2 - x_1)}^2} + {{(y_2 - y_1)}^2}} $ and also keep in mind the parametric equation of ellipse as $x = a\cos \theta ,y = b\sin \theta $.