Question

Earth is dugout to make a well 28m deep and 2.8m in diameter. Find the cost of plastering its inner surface at RS. 4.50 per sq. meter.
(a) RS. 1136.52
(b) RS. 1209.24
(c) RS. 1010.86
(d) None of the above

Answer 1

Hint: The rough figure that represents the dimensions of the well is shown below

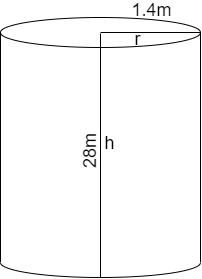
Complete step by step answer:
We are given that the depth of well as 28m
Let us assume that the depth of well as
\[\Rightarrow h=28m\]
We are given that the diameter of well as 2.8m
We know that the radius is half of the diameter.
By using the above condition we get the radius as
\[\begin{align}
  & \Rightarrow r=\dfrac{d}{2} \\
 & \Rightarrow r=\dfrac{2.8}{2}=1.4m \\
\end{align}\]
Now let us find the inner surface area of the well
We know that the formula of curved surface area of the cylinder having radius \['r'\] and height or depth \['h'\] is given as
\[CSA=2\pi rh\]

By using the above formula we get the curved surface area of the well as
\[\begin{align}
  & \Rightarrow CSA=2\times \pi \times 28\times 1.4 \\
 & \Rightarrow CSA=78.4\pi \\
\end{align}\]
Now, by using the value of \[\pi \] as \[\dfrac{22}{7}\] in above equation we get
\[\begin{align}
  & \Rightarrow CSA=78.4\times \dfrac{22}{7} \\
 & \Rightarrow CSA=246.4{{m}^{2}} \\
\end{align}\]
Now, let us assume that the total cost of plastering inside the cylinder as \[C\]
We are given that cost of plastering as RS. 4.50 per sq. meter.
Here, we can see that the cost of plastering for \[1{{m}^{2}}\] is RS. 4.50
By using the above condition we get the cost of plastering for \[246.4{{m}^{2}}\] as
\[\begin{align}
  & \Rightarrow C=246.4\times 4.50 \\
 & \Rightarrow C=1108.8 \\
\end{align}\]
Therefore we can conclude that the cost of plastering for the inside of cylinder is RS. 1108.8
So, option (d) is correct answer.

Note:
Students may do mistake in finding the area to solve this problem by finding the surface area of the cylinder.
The formula for the area of a cylinder having radius \['r'\] and height or depth \['h'\] is given as
\[CSA=2\pi rh\]
By using this formula we find the inner surface area and then we can find the cost of plastering.
We are asked to find the cost of plastering inside the well. This gives the curved surface area of the well.
So, we calculate the curved surface area of the well by using the formula
\[CSA=2\pi rh\]
But students may do mistakes and find the total surface area instead of the curved surface area.
The formula of the total surface area is given as
\[\Rightarrow TSA=2\pi rh+2\pi {{r}^{2}}\]
This gives the wrong answer because we don’t use the plastering for the floor of the well and the top of the well will always be open where there will be no area. So, there is no need to consider the total surface area of the well