Question

Each wheel of a car is of diameter 40cm. Find the time taken by the wheel of the car to rotate by 200 radians if the car moves at the speed of 70km/hr.
[a] 17s
[b] 15.26s
[c] 2.06s
[d] 3.09s

Answer 1

Hint: Calculate the total number of revolutions equivalent to $200$ radians (say a). Calculate the distance covered in one revolution of the wheel. Hence calculate the total distance equivalent to a revolution. This will give the total distance covered. Convert the speed of the car in metre/sec. Using the fact that time (T) is given by $T=\dfrac{S}{v}$, where S is the distance covered and v is the speed. Hence determine the total time taken. Alternatively, calculate the angular velocity of the wheel and hence the time taken to cover $200$ radians

Complete step-by-step answer:
The wheel covers a distance equal to the length of the circumference of the wheel in one revolution.
Given the diameter of the wheel = 40 cm =0.4 m
Hence the radius of the wheel = 0.2m.
We know that the circumference of the circle of radius r is given by $c=2\pi r$
Hence distance covered in one revolution $=2\pi \left( 0.2 \right)=0.4\pi $.
Also, we have $2\pi $ radians is equal to 1 complete revolution.
Hence, we have
$1$ radian is equal to $\dfrac{1}{2\pi }$ revolutions
Hence, we have $200$ radians is equal to $\dfrac{200}{2\pi }=\dfrac{100}{\pi }$ revolutions.
We have distance covered in 1 revolutions $=0.4\pi $
Hence the distance covered in $\dfrac{100}{\pi }$ revolutions $=0.4\pi \times \dfrac{100}{\pi }=40m$
(Conversion shortcut: When converting Km/hr to m/s multiply by $\dfrac{5}{18}$)
Here $v=70km/hr=\dfrac{5}{18}\times 70m{{s}^{-1}}=\dfrac{175}{9}m{{s}^{-1}}$
We know that time (T) is given by $T=\dfrac{S}{v}$, where S is the distance covered and v is the speed.
Hence, we have
$T=\dfrac{40}{175}\times 9=2.06s$
Hence the total time taken to rotate 200 radians is 2.06s.
Hence option [c] is correct.

Note: The speed at the circumference of the wheel = 70km/h $=\dfrac{175}{9}\text{m/sec}$
We know that angular velocity $=\dfrac{\text{Velocity at point P}}{\text{Distance of point P from centre}}$, where P is any point on the wheel. Taking P at the circumference of the wheel as shown, we have

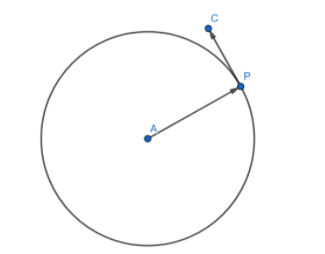
Angular velocity $=\dfrac{\dfrac{175}{9}}{0.2}=\dfrac{875}{9}$ rad/sec
We know that $\theta =\omega t$, where $\theta $ is the amount of angular rotation, $\omega $ is the angular velocity and $t$ is the time taken.
Hence, we have
$t=\dfrac{\theta }{\omega }=\dfrac{200}{\dfrac{875}{9}}=2.06$s.
Hence the total time taken is 2.06s, which is the same as obtained above.
Hence option [c] is correct.