Question

Each side of a square is of length 4 units. The centre of the square is at \[\left( {3,7} \right)\] and one of its diagonal is parallel to \[y = x\] . Then coordinates of its vertices are
A) \[\left( {1,5} \right),\left( {1,9} \right),\left( {8,9} \right),\left( {5,5} \right)\]
B) \[\left( {2,5} \right),\left( {2,7} \right),\left( {4,7} \right),\left( {4,4} \right)\]
C) \[\left( {2,5} \right),\left( {2,6} \right),\left( {3,5} \right),\left( {3,6} \right)\]
D) \[\left( {5,2} \right),\left( {6,2} \right),\left( {5,3} \right),\left( {6,3} \right)\]

Answer 1

Hint:
Here, We have to find the coordinates of vertices of the square using the distance between two points formula. We will first use the slope of the line parallel to the diagonal. Then by using the coordinate of the diagonal, we will be able to find the required coordinate of the vertices of the square.

Formula used:
We will use the following formulas:
1) If two lines are parallel, then \[{m_1} = {m_2}\] where \[{m_1}\] and \[{m_2}\] are the slope of two lines.
2) Equation of the line and point, then \[y - {y_1} = m(x - {x_1})\] where \[({x_1},{y_1})\] are the coordinates of the point and m is the slope of the line.
3) Length of the diagonal of the square = \[\sqrt 2 a\] where a is the side of the square.
4) Distance between two points is given by the formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \] where \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] are the coordinates of two points.

Complete step by step solution:

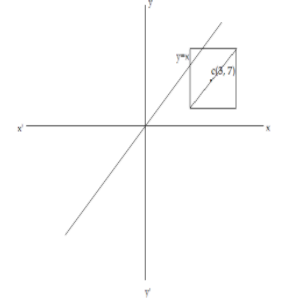
Let ABCD be the square. We are given that the line \[y = x\] is parallel to the diagonal AC.
The line\[y = x\] is of the form \[y = mx + c\] , so we have \[m = 1\]. So we have \[{m_1} = {m_2} = 1\].
Now, we are using the equation of the line and point formula for the line \[y = x\] and the point \[\left( {3,7} \right)\].
\[ \Rightarrow y - 7 = 1(x - 3)\]
Multiplying and equating the terms, we have
\[ \Rightarrow y = x + 4\]
Let \[(h,k)\] be the coordinates of the diagonal. Since \[y = x + 4\] then \[(h,h + 4)\] be the coordinate of the diagonal.
Length of the diagonal of the square \[ = \sqrt 2 a\]
Substituting \[a = 4\] in the above equation, we get
\[ \Rightarrow \] Length of the diagonal of the square \[ = \sqrt 2 \cdot 4 = 4\sqrt 2 \]
Length of the diagonal of the square from the centre of the square \[ = \dfrac{{4\sqrt 2 }}{2} = AP\]
Now we will find the distance between the two points using the formula.
Substituting \[({x_1},{y_1}) = (3,7)\] and \[({x_2},{y_2}) = (h,h + 4)\] in the distance formula, \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \], we get
\[\begin{array}{l}AP = \sqrt {{{\left( {h - 3} \right)}^2} + {{\left( {h + 4 - 7} \right)}^2}} \\ \Rightarrow AP = \sqrt {{{\left( {h - 3} \right)}^2} + {{\left( {h - 3} \right)}^2}} \end{array}\]
Substituting the length of the diagonal , we get
\[ \Rightarrow \dfrac{{4\sqrt 2 }}{2} = \sqrt {{{\left( {h - 3} \right)}^2} + {{\left( {h - 3} \right)}^2}} \]
Squaring on both the sides, we get
\[\begin{array}{l} \Rightarrow \dfrac{{16 \cdot 2}}{4} = {\left( {h - 3} \right)^2} + {\left( {h - 3} \right)^2}\\ \Rightarrow 4 \cdot 2 = {\left( {h - 3} \right)^2} + {\left( {h - 3} \right)^2}\end{array}\]
Multiplying the terms further, we get
\[ \Rightarrow 8 = {\left( {h - 3} \right)^2} + {\left( {h - 3} \right)^2}\]
Now, we will be using the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], we get
\[\begin{array}{l} \Rightarrow 8 = {h^2} + 9 - 6h + {h^2} + 9 - 6h\\ \Rightarrow 8 = 2{h^2} - 12h + 18\end{array}\]
Subtracting like terms, we get
\[\begin{array}{l} \Rightarrow 2{h^2} - 12h + 18 - 8 = 0\\ \Rightarrow 2{h^2} - 12h + 10 = 0\end{array}\]
Dividing by 2 on both the sides, we get
\[ \Rightarrow {h^2} - 6h + 5 = 0\]
By using factorization, we get
\[ \Rightarrow \left( {h - 1} \right)\left( {h - 5} \right) = 0\]
Using zero product property, we get
\[ \Rightarrow h = 1\]
Or
\[ \Rightarrow h = 5\]
Now, we will be substituting the values of \[h\] in the co-ordinates of the diagonal of the square.
Substituting \[h = 1\] in the coordinates, we get
\[\left( {h,h + 4} \right) = (1,1 + 4) = (1,5)\]
So the coordinate of the diagonal of the square be \[\left( {1,5} \right)\] which is correspondingly the coordinate of the vertex of A.
Now to find the coordinate of B we have to add the length of the square 4 units to \[x\] co-ordinate
So, the coordinate of B be \[\left( {5,5} \right)\].
Now to find the coordinate of C we have to add the length of the square 4 units to \[y\] co-ordinate
So, the coordinate of C be \[\left( {5,9} \right)\].
Now to find the coordinate of D we have to add the length of the square 4 units to \[y\] co-ordinate
So, the coordinate of D be \[\left( {1,9} \right)\].

Therefore, the coordinates of vertices of square is \[A\left( {1,5} \right)\], \[B\left( {5,5} \right)\], \[C\left( {5,9} \right)\], \[D\left( {1,9} \right)\]

Note:
We can also find the coordinate of the vertices of the square by using the midpoint formula for the corresponding sides to find the corresponding vertices of the square. A vertex of a geometrical shape is a point where two sides of the shape meet. Vertices usually define a geometric shape, when the same shape is defined inside the coordinate plane.