Question

Each side of a square is \[4\] units. The center of the square is at \[\left( {3,7} \right)\] and one of its diagonals is parallel to \[x = y\]. The coordinates of its vertices are
A.\[\left( {1,5} \right),\left( {1,9} \right),\left( {5,9} \right),\left( {5,5} \right)\]
B.\[\left( {2,5} \right),\left( {2,7} \right),\left( {4,7} \right),\left( {4,4} \right)\]
C.\[\left( {2,5} \right),\left( {2,6} \right),\left( {3,5} \right),\left( {3,6} \right)\]
D.\[\left( {5,2} \right),\left( {6,2} \right),\left( {5,3} \right),\left( {6,3} \right)\]

Answer 1

Hint: We have been given that one diagonal is parallel to \[x = y\], so its slope will also be equal to the slope of this equation. And, the other diagonal is perpendicular to this diagonal (because the diagonals of a square intersect each other at right angles).

Formula Used:
We will use the formula for calculating the slope of a line (say the equation of the line is \[ax + by = c\]), which is given by:
Slope, \[m = - \dfrac{b}{a}\] …(i)
Now it is a known thing that if we have been given the slope (say \[{m_1}\]) of a line, then the slope of a line perpendicular to that line is given by the formula:
\[{m_2} = - \dfrac{1}{{{m_1}}}\] …(ii)

Complete step-by-step answer:

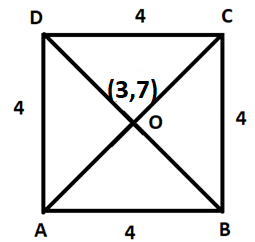
Assume a square ABCD (as shown above) with length of each side given to be \[4\]units.
Consider O to be the point of intersection of the diagonals of the square. The given point of intersection of the diagonals, or we can say the center of the square, is given to be \[(3,7)\].
Now, since we have been given the length of the side of the square to be \[4\]units, we can calculate the length of the diagonal too:
Length of diagonal = \[\sqrt 2 \times \]Length of a side
This is because the two sides and a diagonal form a right-angled triangle with the two equal sides (\[S,S\]) as the base, perpendicular and the diagonal (\[D\]) as the hypotenuse. And we know the relation between hypotenuse, base, perpendicular by the Pythagoras Theorem:
\[{H^2} = {P^2} + {B^2}\]
Hence, \[{D^2} = {S^2} + {S^2}\]
\[{D^2} = 2{S^2}\]
Thus, \[D = \sqrt 2 \times S\]
Hence, the length of the two diagonals (AC, BD) of the square ABCD = \[\sqrt 2 \times 4 = 4\sqrt 2 \]units
Now, both the diagonals are intersected at the center O, hence
\[AO = BO = CO = DO = \dfrac{1}{2}AC = \dfrac{1}{2} \times 4\sqrt 2 = 2\sqrt 2 \]units …(iii)

Now, it is given that one diagonal is parallel to \[y = x\]

In our case, it is the diagonal AC.
AC is parallel to the line with equation \[y = x\] or \[x - y = 0\]
Now, since they are parallel, their slopes are going to be equal but their intercepts are different.
So, the equation of AC is going to be:
\[x - y = k\], with \[k\]as the intercept
Now, since the diagonal passes through \[\left( {3,7} \right)\], we can put in the values in the equation \[x - y = k\]and evaluate for the value of \[k\]:
\[k = 3 - 7 = - 4\]
Hence, the equation of AC is \[y = x + 4\]
Now, the slope of the equation of AC is \[{m_1} = - \dfrac{{{\rm{coefficient of }}y}}{{{\rm{coefficient of }}x}} = - \dfrac{{ - 1}}{1} = 1\]
Using the equation (ii), we can calculate the slope of the equation of diagonal BD, as the two diagonals are perpendicular to each other, we get:
\[{m_2} = - \dfrac{1}{{{m_1}}} = - \dfrac{1}{1} = - 1\]
So, the slope of the equation of diagonal BD, is \[ - 1\].
Now, we know the equation of a line whose slope is \[m\], is given by:
\[y = mx + c\]
Here, we have slope of diagonal BD \[ = - 1\], so the equation of diagonal BD can be represented as:
\[y = \left( { - 1} \right)x + c\]
$\Rightarrow$ \[y = - x + c\]
Taking all the variables to one side,
\[x + y - c = 0\] …(iv)
Now, diagonal BD also passes through the center whose coordinates are known to us \[\left( {3,7} \right)\], so:
\[3 + 7 - c = 0\]
$\Rightarrow$ \[10 - c = 0\]
Solving for the value of c, we get \[c = 10\]
Putting \[c = 10\] in the equation (iv), we get
\[x + y - 10 = 0\]
So, the equation of diagonal BD is \[y = 10 - x\]
and the equation of diagonal AC is \[y = x + 4\]
Now, vertices A and C lie on the diagonal AC, so the two points have coordinates which follow the relation:
\[{\rm{A}} = \left( {h,h + 4} \right)\]
Now, using the distance formula we can calculate the length of OA:
Distance formula between two points \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)\], \[d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} \]
\[O\left( {3,7} \right)\] and \[A\left( {h,h + 4} \right)\]
Now, \[OA\] = \[\sqrt {{{\left( {h - 3} \right)}^2} + {{\left( {h + 4 - 7} \right)}^2}} \]
$\Rightarrow$ \[OA\]= \[\sqrt {{{\left( {h - 3} \right)}^2} + {{\left( {h - 3} \right)}^2}} \]
$\Rightarrow$ \[OA\]= \[\sqrt {2{{\left( {h - 3} \right)}^2}} \]
Taking the square part out of the square root bracket:
$\Rightarrow$ \[OA\]= \[\left( {h - 3} \right)\sqrt 2 \]
Now, from equation (iii) we have,
$\Rightarrow$ \[OA = 2\sqrt 2 \]
So, equating the two equations,
$\Rightarrow$ \[\left( {h - 3} \right)\sqrt 2 = 2\sqrt 2 \]
Canceling the \[\sqrt 2 \] from the two sides, we get
\[h - 3 = 2\]
Thus, \[h = 5\]
Hence, the coordinates of the vertex \[A\]is \[\left( {5,5 + 4} \right) = \left( {5,9} \right)\]
Now, for calculating the coordinates of the vertex \[C\] can be calculated by using the point \[O\] as the
mid-point between \[A\] and \[C\], we get:
Let the coordinates of point \[C\] be \[\left( {l,m} \right)\], so:
\[\dfrac{{l + 5}}{2} = 3\] and \[\dfrac{{m + 9}}{2} = 7\]
So, \[l = 1\] and \[m = 5\]
Hence, the coordinates of vertex \[C\] is \[\left( {1,5} \right)\].
Similarly using the equation of BD, we can calculate the coordinates of B and D, and we get the two as:
Coordinates of \[B = \left( {1,9} \right)\]
and, coordinates of \[D = \left( {5,5} \right)\]
Hence, the answer of this question is A \[\left( {1,5} \right),\left( {1,9} \right),\left( {5,9} \right),\left( {5,5} \right)\]

Note: The way to solve this question is by drawing a figure and then using the figure as a reference. The only thing that is required is to remember the basic formulae and know where and how to apply them. The figures help in visualizing the problem and grasping the concept better.