Question

Each side of a rhombus is \[\text{14}\] in. long. Two of the sides form a \[\text{6}0{}^\circ \] degree angle, how do you find the area of the rhombus?

Answer 1

Hint: To get area of a rhombus, we will use the following formula:
\[\Rightarrow \text{Area of Rhombus }\left( \text{A} \right)\text{ }={{s}^{2}}\sin \alpha \]
Where, $s$ is a side of rhombus and $\alpha $ is measure of any interior angle. Since, each side of the rhombus is equal, $s=\text{14}$ and the given angle will be $\alpha =\text{6}0{}^\circ $ . After applying this value in the above formula, we will get the area of rhombus.

Complete step-by-step answer:
Given that side of rhombus $=14$ in. and an angle formed by two sides $=60{}^\circ $

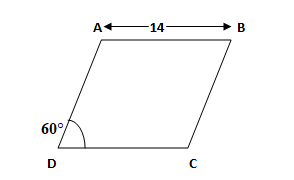
Since, each side of rhombus is equal to each other, so:
$\Rightarrow AB=BC=CD=DA=14=s$
An angle formed by two consecutive sides of rhombus $=60{}^\circ =\alpha $
Now, we have the formula for finding the area of the given rhombus as:
\[\Rightarrow \text{Area of Rhombus }\left( \text{A} \right)\text{ }={{s}^{2}}\sin \alpha \]
Since, we already have the value of $s$ and $\alpha $ , we will use this values in the above equation to get the area of rhombus as:
\[\text{Area of Rhombus }\left( \text{A} \right)\text{ }={{\left( 14 \right)}^{2}}\sin \left( 60{}^\circ \right)\]
Now, we will expand the equation as:
\[\text{Area of Rhombus }\left( \text{A} \right)\text{ }=14\times 14\times \sin \left( 60{}^\circ \right)\]
Since, we know that the value of \[\sin \left( 60{}^\circ \right)\] is $\dfrac{\sqrt{3}}{2}$ . We will put this value in the above equation, then the equation will be as;
\[\text{Area of Rhombus }\left( \text{A} \right)\text{ }=14\times 14\times \dfrac{\sqrt{3}}{2}\]
After doing necessary calculation like multiplication of $14$ and $14$ is $196$ , the above equation will be as:
\[\text{Area of Rhombus }\left( \text{A} \right)\text{ }=196\times \dfrac{\sqrt{3}}{2}\]
Now, the multiplication makes the above equation as:
\[\text{Area of Rhombus }\left( \text{A} \right)\text{ }=98\sqrt{3}\]
Hence, applying the required calculation in the formula, we had the area of rhombus is \[98\sqrt{3}\text{ in}{{\text{.}}^{2}}\] .

Note: Here, we will verify that if our solution is correct or not in the following way by using formula of area of rhombus as:
\[\Rightarrow \text{Area of Rhombus }\left( \text{A} \right)\text{ }={{s}^{2}}\sin \alpha \]
Here, we will try to find the side of rhombus by putting the value of area of Rhombus and angle formed by two sides as:
\[\Rightarrow \text{98}\sqrt{3}\text{ }={{s}^{2}}\sin 60{}^\circ \]
Since, we have the value $\dfrac{\sqrt{3}}{2}$ for\[\sin 60{}^\circ \]. We will use it in the above equation as:
\[\Rightarrow \text{98}\sqrt{3}\text{ }={{s}^{2}}\times \dfrac{\sqrt{3}}{2}\]
Here, we will divide by $\sqrt{3}$ in the above equation:
\[\Rightarrow \dfrac{\text{98}\sqrt{3}}{\sqrt{3}}\text{ }=\dfrac{{{s}^{2}}\times \dfrac{\sqrt{3}}{2}}{\sqrt{3}}\]
Now, the above equation will be as:
\[\Rightarrow \text{98 }={{s}^{2}}\times \dfrac{1}{2}\]
After doing required calculation, the above equation will be as:
\[\Rightarrow {{s}^{2}}=\text{98 }\times 2\]
\[\Rightarrow {{s}^{2}}=196\]
Taking square root both sides in the above equation, we will have:
\[\Rightarrow s=14\] in.
Since, we got the given side of the rhombus by putting the area of rhombus. Hence, the calculation is correct.