Question

Each of the equal sides of an isosceles triangle is \[2cm\] more than its height and the base of the triangle is \[12cm\] . Find the area of the triangle.

Answer 1

Hint: In this problem, the isosceles triangle has each of the equal sides more than its height and the base values are mentioned. Isosceles triangle is defined as a triangle whose two sides are equal and one side is unequal. So we need to calculate the area of the triangle from the given values.

Complete step-by-step answer:
In the given problem, the measurement is represented by a diagram is mentioned below

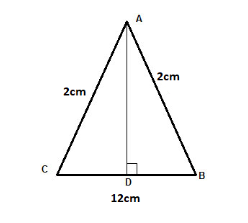
Let the height of the triangle be ‘h’
Each of the equal sides are measured as \[a = (h + 2)cm,\]
Base of the triangle, \[b = 12cm\]
According to the area of isosceles triangle, we need to find the height of the triangle by the formula is given below,
Area of the isosceles triangle \[ = \dfrac{1}{4}b\sqrt {4{a^2} - {b^2}} \]
Area of the triangle \[ = \dfrac{1}{2}bh\]
Now,
Area of the triangle \[ = \] Are of the isosceles triangle
 \[\dfrac{1}{2}bh = \dfrac{1}{4}b\sqrt {4{a^2} - {b^2}} \]
By substitute all the values in further calculation, we get
 \[\dfrac{1}{2}(12)h = \dfrac{1}{4}(12)\sqrt {4{{(h + 2)}^2} - {{(12)}^2}} \]
By simplify in further, we get
 \[6h = 3\sqrt {4{{(h + 2)}^2} - {{(12)}^2}} \]
On compare the algebraic formula \[{(a + b)^2} = {a^2} + {b^2} + 2ab\] with the height \[{(h + 2)^2}\] ,we get \[{(h + 2)^2} = {h^2} + {2^2} + 2(h \times 2)\]
Now, we get
 \[
  6h = 3\sqrt {4({h^2} + {2^2} + 2(2)h) - 144} \\
  \dfrac{{6h}}{3} = \sqrt {4({h^2} + 4 + 4h) - 144} \;
 \]
By performing arithmetic operation on both sides, we have
 \[2h = \sqrt {4{h^2} + 16 + 16h - 144} \]
To simplify in further
 \[2h = \sqrt {4{h^2} + 16h - 128} \]
Take square on both sides, we get
 \[
  {(2h)^2} = {(\sqrt {4{h^2} + 16h - 128} )^2} \\
  4{h^2} = 4{h^2} + 16h - 128 \;
 \]
By further simplification
 \[
  4{h^2} - 4{h^2} - 16h = - 128 \\
   - 16h = - 128 \;
 \]
To find the final value, we get
 \[h = 8cm\]
To calculate the area of the triangle is \[\dfrac{1}{2}bh = \dfrac{1}{2} \times 12 \times 8 = 48\;c{m^2}\]
Therefore, the area of the triangle is \[48\;c{m^2}\] .
So, the correct answer is “ \[48\;c{m^2}\] ”.

Note: Here, we use the area of isosceles triangle and triangle to find the height by the formula is given below,
Area of the isosceles triangle \[ = \dfrac{1}{4}b\sqrt {4{a^2} - {b^2}} \] , Area of the triangle \[ = \dfrac{1}{2}bh\] .Isosceles triangle is defined as a triangle whose two sides are equal and one side is unequal. So we need to calculate the area of the triangle from the given values.