
Each capacitor in the circuit shown is a \[1F\] capacitor. What would be the equivalent capacitance between A and B
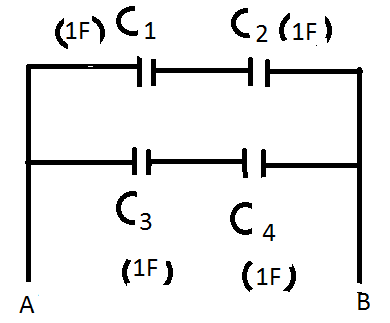
\[(A)0.5F\]
\[(B)1F\]
\[(C)2F\]
\[(D)4F\]
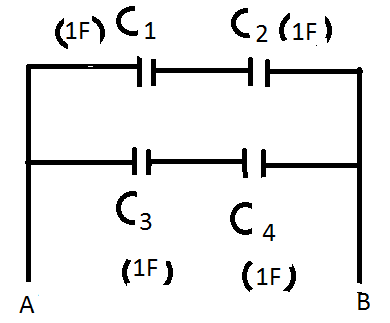
Answer
508.5k+ views
Hint: It can be solved by identifying which capacitors are in series and which sets are in parallel by using a formula for the equivalent capacitance for series and parallel combinations, we can get the equivalent capacitance between the required points.
Formula used:
Each capacitance of each pair of capacitance in series = \[\dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}F\]
Complete step by step answer:
A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit.
A \[1\]-farad capacitor can store one coulomb (coo-lamb) of charge at \[1\] volt. One amp represents a rate of electron flow of \[1\] coulomb of electrons per second, so a \[1\]-farad capacitor can hold \[1\] amp-second of electrons at \[1\] volt. A \[1\]-farad capacitor would typically be pretty big.
A one-farad modern super-capacitor. The farad (symbol: F) is the SI-derived unit of electrical capacitance, the ability of a body to store an electrical charge. It is named after the English physicist Michael Faraday. In SI base units \[1F\] = \[1{s^4} \cdot {A^2} \cdot {m^{ - 2}} \cdot k{g^{ - 1}}.\]
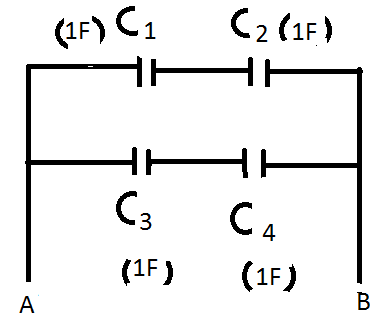
Where,
\[{C_1} = 1F\]
\[{C_2} = 1F\]
\[{C_3} = 1F\]
\[{C_4} = 1F\]
Each capacitance of each pair of capacitance in series = \[\dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}F\]
Each capacitance of each pair of capacitance in series = \[\dfrac{{1 \times 1}}{{1 + 1}}F = 0.5F\]
The two series combination is connected in parallel. Hence the net capacitance becomes \[0.5F + 0.5F = 1F\].
So, the correct answer is “Option C”.
Note: The equivalent capacitance is the net total capacitance of the capacitor connected in a circuit.
The equivalent has a large plate area and can therefore hold more charge than the individual capacitor.
Formula used:
Each capacitance of each pair of capacitance in series = \[\dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}F\]
Complete step by step answer:
A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit.
A \[1\]-farad capacitor can store one coulomb (coo-lamb) of charge at \[1\] volt. One amp represents a rate of electron flow of \[1\] coulomb of electrons per second, so a \[1\]-farad capacitor can hold \[1\] amp-second of electrons at \[1\] volt. A \[1\]-farad capacitor would typically be pretty big.
A one-farad modern super-capacitor. The farad (symbol: F) is the SI-derived unit of electrical capacitance, the ability of a body to store an electrical charge. It is named after the English physicist Michael Faraday. In SI base units \[1F\] = \[1{s^4} \cdot {A^2} \cdot {m^{ - 2}} \cdot k{g^{ - 1}}.\]
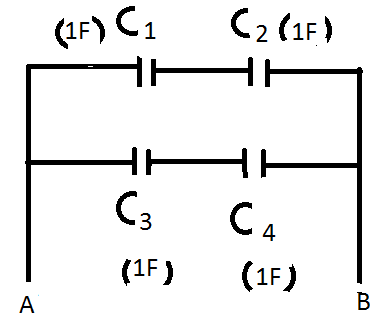
Where,
\[{C_1} = 1F\]
\[{C_2} = 1F\]
\[{C_3} = 1F\]
\[{C_4} = 1F\]
Each capacitance of each pair of capacitance in series = \[\dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}F\]
Each capacitance of each pair of capacitance in series = \[\dfrac{{1 \times 1}}{{1 + 1}}F = 0.5F\]
The two series combination is connected in parallel. Hence the net capacitance becomes \[0.5F + 0.5F = 1F\].
So, the correct answer is “Option C”.
Note: The equivalent capacitance is the net total capacitance of the capacitor connected in a circuit.
The equivalent has a large plate area and can therefore hold more charge than the individual capacitor.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




