Question

E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If $AD\bot BC$ and $EF\bot AC$, prove that $\Delta ABD\sim \Delta ECF$.

Answer 1

- Hint: In this question, we should first construct an appropriate figure according to the given information which would be helpful in order to solve the question. The figure should contain an isosceles triangle ABC and produced CB with a point E on CB produced from where a perpendicular EF to AC produced must be drawn and also AD perpendicular to BC must be built. Then we can use the Angle-Angle (A-A) criterion to prove that $\Delta ABD\sim \Delta ECF$.

Complete step-by-step solution -

It is given that E is a point on side CB produced of an isosceles triangle ABC with AB=AC which implies that $\angle ACB=\angle ABC$,$AD\bot BC$implies that $\angle ADB={{90}^{\circ }}$and $EF\bot AC$ which implies $\angle CFE={{90}^{\circ }}$. Let us first build an appropriate diagram based on the given information.

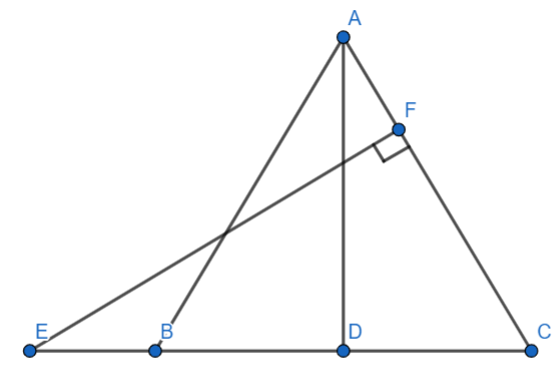
Here, we are given to prove that $\Delta ABD\sim \Delta ECF$. The proof is as follows:
In $\Delta ACD\text{ }and\text{ }\Delta ECF,$
$\angle ACD=\angle ECF$ (Common)
$\angle ADC=\angle CFE$ (Each ${{90}^{\circ }}$)
$\Rightarrow \Delta ACD\sim \Delta ECF$(A-A similarity criterion) ………… (1.1)
Now, $\angle ACB=\angle ABC$ (As, angles opposite in equal sides in an isosceles triangle are equal)………(1.3)
In $\Delta ABD\text{ }and\text{ }\Delta ECF,$
$\angle ABC=\angle ACB$ (Proved in equation 1.2)
$\angle ADC=\angle CFE$ (Each ${{90}^{\circ }}$)
$\Rightarrow \Delta ABD\sim \Delta ECF$ (A-A similarity criterion) ………… (1.3)
Hence, we have arrived at our required answer that is $\Delta ABD\sim \Delta ECF$.

Note: In the diagram we must be careful about the given information and construct it the correct way as it plays a great role in solving the question. So, even a small mistake in the figure will lead us to an incorrect and unwanted result and cause difficulties in solving.