
During the first half of the motion, applied force transfers more energy to the
A. Kinetic Energy
B. Potential energy
C. Equal to both
D. None of this

Answer
476.1k+ views
Hint: At first, the kinetic energy has to be noted due to the whole motion. The work-energy theorem is used here to find the maximum displacement of the spring shown in the figure. To find the displacement at the first half of the motion just half the maximum displacement.
Next, the potential energy and kinetic energy have to be calculated at this range of displacement and the answer will be revealed.
Formula used:
The work-energy theorem between \[x = 0\] to \[x = {x_{max}}\]
\[{W_1} + {W_2} = 0\]
\[{W_1} = Fx\],
Where, \[F = \]Applied force.
\[{W_2} = \dfrac{1}{2}{\text{ }}k\left( {{0^2} - {x^2}} \right)\]
Complete step by step answer:
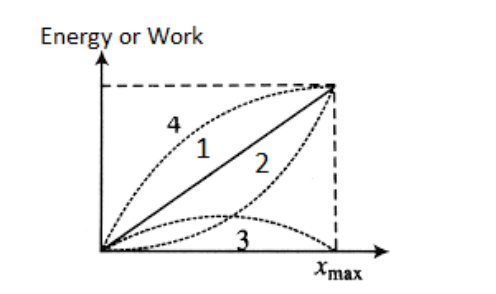
From \[x = 0\] to \[x = {x_{max}}\]
\[K.E = 0\]
Applying the work-energy theorem between \[x = 0\] to \[x = {x_{max}}\]
\[{W_1} + {W_2} = 0\]
\[ \Rightarrow F{x_{max}} + \dfrac{1}{2}{\text{ }}k\left( {{0^2} - {x_{max}}^2} \right) = 0\]
\[ \Rightarrow {x_{max}} = \dfrac{{2F}}{k}\]
So the first half is concerned with $0 \leqslant x \leqslant \dfrac{F}{k}$
At, $x = \dfrac{F}{k}$
${U_1} = $ The potential energy = Energy stored in the spring = \[\dfrac{1}{2}k{\left( {\dfrac{F}{k}} \right)^2} = \dfrac{{{F^2}}}{{2k}}\]
The kinetic energy At, $x = \dfrac{F}{k}$ is ${K_1}$.
To calculate this we again apply the work-energy theorem between \[x = 0\] to $x = \dfrac{F}{k}$
\[ \Rightarrow {W_1} + {W_2} = {K_1} - 0\]
\[ \Rightarrow F \times \dfrac{F}{k} + \dfrac{1}{2}{\text{ }}k\left[ {{0^2} - {{\left( {\dfrac{F}{k}} \right)}^2}} \right] = {K_1}\]
\[ \Rightarrow \dfrac{{{F^2}}}{k} - \dfrac{{{F^2}}}{{2k}} = {K_1}\]
\[ \Rightarrow {K_1} = \dfrac{{{F^2}}}{{2k}}\]
\[ \therefore {K_1} = {U_1}\]
So, we get that the kinetic energy is equal to the stored energy or potential energy at the first half of the motion.
Hence, the right answer is in option C.
Note: Potential energy is energy that keeps – or preserved - in an object or substance. This keeps energy relies on the position, arrangement, or state of the item or substance. Spring P.E. may be a variety of hold on energy, very similar to gravitational P.E. or electrical P.E., one related to springs and elastic objects. The kinetic energy compressed the spring that has been changed into P.E.. After we leave the spring, the hold on P.E. is changed into kinetic energy.
Next, the potential energy and kinetic energy have to be calculated at this range of displacement and the answer will be revealed.
Formula used:
The work-energy theorem between \[x = 0\] to \[x = {x_{max}}\]
\[{W_1} + {W_2} = 0\]
\[{W_1} = Fx\],
Where, \[F = \]Applied force.
\[{W_2} = \dfrac{1}{2}{\text{ }}k\left( {{0^2} - {x^2}} \right)\]
Complete step by step answer:

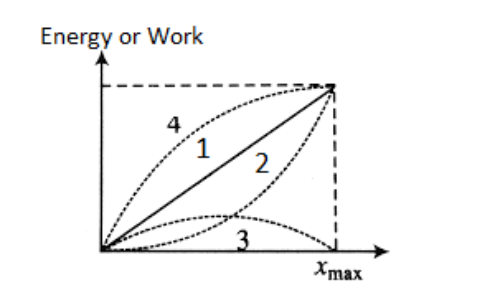
From \[x = 0\] to \[x = {x_{max}}\]
\[K.E = 0\]
Applying the work-energy theorem between \[x = 0\] to \[x = {x_{max}}\]
\[{W_1} + {W_2} = 0\]
\[ \Rightarrow F{x_{max}} + \dfrac{1}{2}{\text{ }}k\left( {{0^2} - {x_{max}}^2} \right) = 0\]
\[ \Rightarrow {x_{max}} = \dfrac{{2F}}{k}\]
So the first half is concerned with $0 \leqslant x \leqslant \dfrac{F}{k}$
At, $x = \dfrac{F}{k}$
${U_1} = $ The potential energy = Energy stored in the spring = \[\dfrac{1}{2}k{\left( {\dfrac{F}{k}} \right)^2} = \dfrac{{{F^2}}}{{2k}}\]
The kinetic energy At, $x = \dfrac{F}{k}$ is ${K_1}$.
To calculate this we again apply the work-energy theorem between \[x = 0\] to $x = \dfrac{F}{k}$
\[ \Rightarrow {W_1} + {W_2} = {K_1} - 0\]
\[ \Rightarrow F \times \dfrac{F}{k} + \dfrac{1}{2}{\text{ }}k\left[ {{0^2} - {{\left( {\dfrac{F}{k}} \right)}^2}} \right] = {K_1}\]
\[ \Rightarrow \dfrac{{{F^2}}}{k} - \dfrac{{{F^2}}}{{2k}} = {K_1}\]
\[ \Rightarrow {K_1} = \dfrac{{{F^2}}}{{2k}}\]
\[ \therefore {K_1} = {U_1}\]
So, we get that the kinetic energy is equal to the stored energy or potential energy at the first half of the motion.
Hence, the right answer is in option C.
Note: Potential energy is energy that keeps – or preserved - in an object or substance. This keeps energy relies on the position, arrangement, or state of the item or substance. Spring P.E. may be a variety of hold on energy, very similar to gravitational P.E. or electrical P.E., one related to springs and elastic objects. The kinetic energy compressed the spring that has been changed into P.E.. After we leave the spring, the hold on P.E. is changed into kinetic energy.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




