Question

During a rainy day, rain is falling vertically with a velocity $2m{s^{ - 1}}.$ A boy at rest starts his motion with a constant acceleration of $2m{s^{ - 2}}$ along a straight road. Find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain always falls parallel to the axis of the umbrella.

Answer 1

Hint: Follow the given word statements step by step and convert them in the mathematical expressions. Use formula for velocity as the product of the acceleration and time, ${v_b} = a \times t$ and use derivatives to find the rate of change of angle with respect to time for the required solution.

Complete step by step answer:
Let the velocity of rain falling be ${v_r} = 2m/s$
Acceleration, $a = 2m/{s^2}$
Velocity of boy be ${v_b} = a \times t$
Place the values in the above equation –
${v_b} = 2t$
Velocity of rain with respect to boy is $\overrightarrow {{v_{rb}}} = \overrightarrow {{v_r}} - \overrightarrow {{v_b}} $

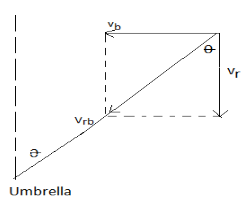
From the above figure, we can find $\tan \theta = \dfrac{{{v_b}}}{{{v_r}}}$
Place the known values in the above equation –
$\tan \theta = \dfrac{{2t}}{2}$
By simplification- we get,
$\tan \theta = t{\text{ }}.....{\text{(a)}}$
We have to find out – the rate, at which an angle changes vertically with respect to time, $\dfrac{{d\theta }}{{dt}} = ?$
Now, take derivative of the equation (a) with respect to “t” -
\[
  \dfrac{{d\tan \theta }}{{dt}} = \dfrac{{dt}}{{dt}}{\text{ }} \\
  {\text{ }}\dfrac{{d\tan \theta }}{{dt}} = 1{\text{ }} \\
 \]
The above equation can be re-written as –
$\dfrac{{d\tan \theta }}{{d\theta }} \times \dfrac{{d\theta }}{{dt}} = 1$
Now, we know that derivative of $\tan \theta = {\sec ^2}\theta $
${\sec ^2}\theta \times \dfrac{{d\theta }}{{dt}} = 1$
Now make the required unknown angle the subject –
$\dfrac{{d\theta }}{{dt}} = \dfrac{1}{{{{\sec }^2}\theta }}$
By property - ${\sec ^2}\theta = 1 + {\tan ^2}\theta $
$ \Rightarrow \dfrac{{d\theta }}{{dt}} = \dfrac{1}{{1 + {{\tan }^2}\theta }}$
Place the value of $\tan \theta $ in the above equation
$ \Rightarrow \dfrac{{d\theta }}{{dt}} = \dfrac{1}{{1 + {t^2}}}$
Hence, the required answer - the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain always falls parallel to the axis of the umbrella is $\dfrac{{d\theta }}{{dt}} = \dfrac{1}{{1 + {t^2}}}$.

Note:
Correct application of formula and its substitution is the most important factor in this question. Also, the correct application of the derivative gives the right answer. Remember the basic derivative of the trigonometric functions.